第３７９問の解答

問題［推理（規則性）］

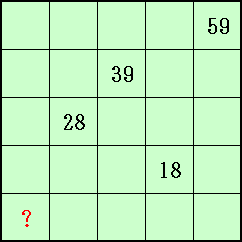問題図 左図のような５×５のマス目があります。

このマス目の各空欄に数字を記入して、各縦の列および各横の列がすべて等差数列になるようにします。

このとき、図の？の欄に当てはまる数字を求めてください。

解答例１

トトロ＠Ｎさん、はなうさん、涼音さん、遠い山のぽきょぽんさん、 他

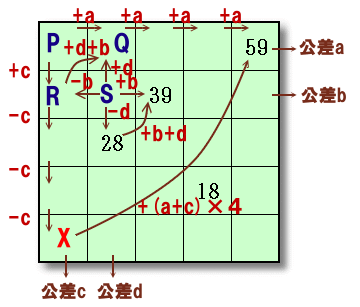
左上にある４個のマス目の数字をP、Q、R、Sとおき、
上から１、２行目の公差（左→右）をａ、ｂ、左から１、２列目の公差（下→上）をｃ、ｄとします。

参考図１

Ｓから見て、
・右への増分＝＋ｂ
・左への増分＝−ｂ
・上への増分＝＋ｄ
・下への増分＝−ｄ

従って、
　Ｑ−Ｒ＝ｂ−（−ｄ）＝ｂ＋ｄ＝３９−２８＝１１

また、Ｐから見て、
・右への増分＝＋ａ
・下への増分＝−ｃ

よって、
　Ｑ−Ｒ＝ａ−（−ｃ）＝ａ＋ｃ＝１１

さて、Ｐから見て、
・４つ右へは＋４ａ
・４つ下へは−４ｃ

よって、
　５９−Ｘ＝４ａ−（−４ｃ）＝４（ａ＋ｃ）＝４４

従って、
　Ｘ＝５９−４４＝１５
と求まります。　

答：　１５

以上

解答例２

中村明海さん、すてっぷさん、小学名探偵さん、浜　たろうさん、まるケンさん、他

参考図２

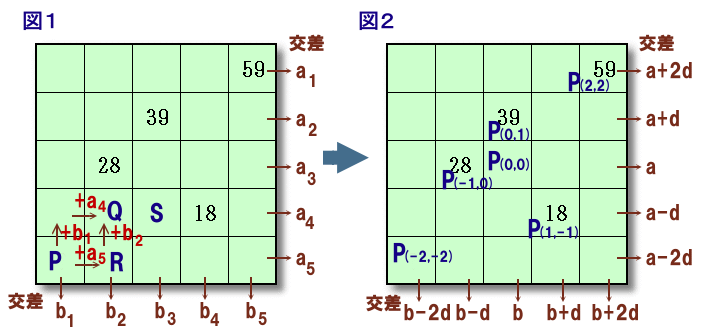
下からi行目の公差（左→右）をａi、左からi列目の公差（下→上）をbiとします。 （図１）

解答例１と同様にして、
Ｐ→Ｑの増分＝ａ5＋ｂ2＝ｂ1＋ａ4
よって、　ｂ2−ｂ1＝ａ4−ａ5

R→Sの増分＝ａ5＋ｂ3＝ｂ2＋ａ4
よって、　ｂ3−ｂ2＝ａ4−ａ5

同様にして、
　ｂ4−ｂ3＝ｂ5−ｂ4＝ａ4−ａ5

従って、ｂ1、ｂ2、ｂ3、ｂ4、ｂ5は差がすべて等しい(＝ａ4−ａ5)ので等差数列と分かります。

全く同様に、
　ａ4−ａ5＝ａ3−ａ4＝ａ2−ａ3＝ａ1−ａ2＝ｂ2−ｂ1
従って、ａ1、ａ2、ａ3、ａ4、ａ5も差がすべて等しい(＝ｂ2−ｂ1)ので等差数列となり、
両者の公差は等しい（ｄとします）ことが分かります。

さて、中央のマス目を原点にして、右にｘ、上へｙだけ進んだマス目を(x,y)、
その上の数字をＰ(x,y)と表わします。

また、ａ3＝ａ、ｂ3＝ｂとおくと、各公差は、
　ａ-2d、ａ-d、ａ、ａ＋d、ａ＋２d、およびｂ-2d、ｂ-d、ｂ、ｂ＋d、ｂ＋２d
と表すことができます。

すると、
　Ｐ(0,0)→Ｐ(x,0)の増分＝ａｘ、
　Ｐ(ｘ,0)→Ｐ(x,ｙ)の増分＝(b＋ｄｘ）ｙ、
よって、
　Ｐ(x,ｙ)＝Ｐ(0,0)＋ａｘ＋ｂｙ＋ｄｘｙ　・・・　（１）
となります。

さて、対角線上の２点（-ｋ、-ｋ）から（ｋ、ｋ）の増分を求めてみましょう。

（１）より、
　Ｐ(k,k)＝Ｐ(0,0)＋ａk＋ｂk＋ｄk2　・・・　（３）
　Ｐ(-k,-k)＝Ｐ(0,0)-ａk-ｂk＋ｄk2　・・・　（４）

（３）−（４）より、
　Ｐ(k,k)−Ｐ(-k,-k)＝２（ａ＋ｂ）ｋ　・・・　（５）
となります。

ところで、（１）より、
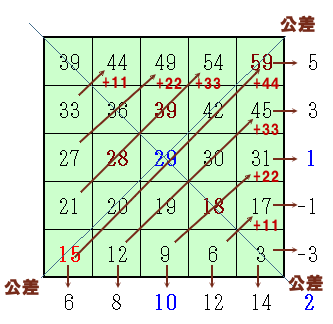
　Ｐ(0,1)＝Ｐ(0,0)＋ｂ＝３９　・・・　（６）
　Ｐ(-1,0)＝Ｐ(0,0)−ａ＝２８　・・・　（７）
したがって、（６）−（７）より、
　ａ＋ｂ＝３９−２８＝１１

（５）より、
　Ｐ(k,k)−Ｐ(-k,-k)＝２２ｋ

とくに、
　Ｐ(2,2)−Ｐ(-2,-2)＝２２×２

よって、
　求めるマス目の数字＝５９−４４＝１５
となります。

なお、
　Ｐ(2,2)＝Ｐ(0,0)＋２ａ＋２b＋４ｄ＝５９　・・・　（８）
　Ｐ(1,-1)＝Ｐ(0,0)＋ａ−b−ｄ＝１８　・・・　（９）
なので、（６）、（７）、（８）、（９）の４元連立方程式を解くと、
 Ｐ(0,0)=２９、ａ＝１０、ｂ＝１、ｄ＝２
を得ます。

参考図２−２

（参考）
左上から右下への対角線を対称軸とする２点の数字の差：
　Ｐ(x,ｙ)−Ｐ(-y,-x)＝ａｘ＋ｂｙ＋ｄｘｙ-（−ａｙ−ｂｘ＋ｄｘｙ）＝（ａ＋ｂ）（ｘ＋ｙ）＝１１（ｘ＋ｙ）

左下から右上への対角線を対称軸とする２点の数字の差：
　Ｐ(x,ｙ)−Ｐ(y,x)＝ａｘ＋ｂｙ＋ｄｘｙ-（ａｙ＋ｂｘ＋ｄｘｙ）＝（ａ-ｂ）（ｘ＋ｙ）＝９（ｘ＋ｙ）

解答例３

ゴンともさん、小西孝一さん、さん、他

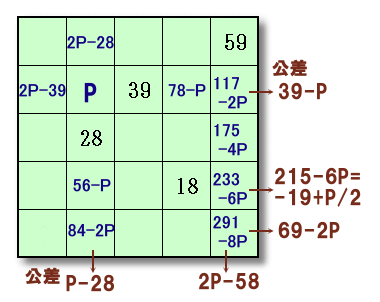
左上から２行２列目の数字をＰとします。

参考図３

２行目の公差(左→右)＝３９−Ｐなので、
　２行目：２Ｐ−３９、Ｐ、３９、７８−Ｐ、１１７−２Ｐ
となります。

また、２列目の公差(下→上)＝Ｐ−２８なので、
　２列目：８４−２Ｐ、５６−Ｐ、２８、Ｐ、２Ｐ−２８
となります。

さらに、５列目の公差(下→上)＝５９−（１１７−２Ｐ）＝２Ｐ−５８なので、
　５列目：２９１−８Ｐ、２３３−６Ｐ、１７５−４Ｐ、１１７−２Ｐ、５９
となります。

なお、４行目の公差は、
　｛１８−（５６−Ｐ）｝×１/２＝２３３−６Ｐ−１８
から
　Ｐ＝３６
を得ます。

したがって、５行目の公差は、
　｛（２９１−８Ｐ）−（８４−２Ｐ）｝×１/３
＝６９−２Ｐ

よって、
　求める数字＝（８４−２Ｐ）−（６９−２Ｐ）＝１５
と求まります。

ということで、Ｐの値によらず求める数字は常に１５であることが分かります。

なお、４行目の公差は、
　｛１８−（５６−Ｐ）｝×１/２＝２３３−６Ｐ−１８
となり、
　Ｐ＝３６
を得ます。

（その他の解法）