第380問の解答
問題[場合の数]
|
|
|
|
|
|
4組(男女8人)のカップルが円卓で昼食会を開くことになりました。 円卓の周りには8つのイスがあって、8人はどれかのイスに座ることになります。 このとき、8人のイスへの座り方は何通りあるでしょうか。 |
|
|
|
|
|
解答例1
Taroさん、呑さん、ヌオの母さん、AЯOTさん、みかんさん、拓パパさん、CRYING DOLPHINさん、はなうさん、DrKさん、小西孝一さん、小学名探偵さん、M.Hossieさん、ミミズクはくず耳さん、大岡 敏幸さん、ポケモンハルカさん、 他多数
女性または男性が1人でいると、両隣が異性なのでどちらかは自分の恋人ではありえないので不適。よって、女性、男性とも2人以上で固まっていることになります。 (以降、固まりのことを連鎖と呼ぶことにします)
また、女性連鎖、男性連鎖は、互い違いに並ぶことになるので個数は等しい。・・・(1)
カップルが4組の場合、女性連鎖、男性連鎖は、
4個(ケース1)か、2個+2個(ケース2)
の2通りになります。各ケースの数え方はいろいろありますが、次の方法が分かりやすいでしょう。
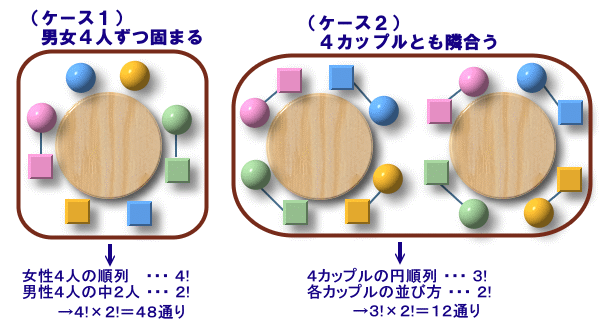
(ケース1)
・まず、女性4人を並べます。 ・・・ 4!=4×3×2×1=24通り
・男性4人のうち、両端の2人は自分の恋人の隣に座ります。
残り2人の並び方 ・・・ 2!=2×1=2通り
→24×2=48通り(ケース2)
・4組のカップルの並び方は4組の円順列 ・・・ 3!=3×2×1=6通り
・各カップル内の女性・男性の並び方は全て同じ ・・・ 2!=2×1=2通り
→6×2=12通りよって、
座り方合計=48+12=60通り
と求まります。答: 60通り
以上
解答例2
小学名探偵さん、中村明海さん、ほげさん、他
この問題の一般化に3人の方が取り組まれました。その結果をご紹介いたします。
カップルがn組(n≧2)のときの座り方をP(n)とします。
解答例1の(1)から、女性連鎖、男性連鎖がk個(1≦k≦n×1/2)のときの座り方を、Q(n、k)と すると、
P(n)=ΣQ(n、k)
と表すことができます。まず、Q(n、k)を求めます。
(1)k個ずつある女性連鎖、および男性連鎖で、それぞれの両端にいる人たちは、恋人と隣り合っています。逆に恋人と隣り合っているカップルは、互いに女性連鎖または男性連鎖の端にいます。これら2k組のカップルをn組のカップルから選ぶ並び方は、
・・・ nC2k通り(2)選ん2k組のカップルをの並び方は、 ちょうど解答例1のケース2と同じになるので
・・・ (2k-1)!×2!通り(3)残りの女性(n−2k)人は、連鎖の内側にいることになります。
まず1人目を並べることのできる位置は、n個の連鎖(2人ずつ並んでいる)のうち、
いずれかの間なので ・・・ k通り2人目は、2人ずつ並ぶ女性の組は1つ増えて(k+1)組となるので、・・・ (k+1)通り
以下同様にして、最後の女性は(n-2k)人目なので、
・・・ {k+(n−2k)−1}=(n-k-1)通り従って、
合計=k×(k+1)×(k+1)×・・・×(n-k-1)=(n-k-1)!/(k-1)!通り(4)残りの男性(n−2k)人の並べ方も(3)と全く同じなので、
・・・ (n-k-1)!/(k-1)!通りよって以上から、
Q(n、k)=nC2k×(2k-1)!×2!×{(n-k-1)!/(k-1)!}2 通り
となり、
P(n)=Σ(k=1..[n/2]) nC2k×(2k-1)!×2!×{(n-k-1)!/(k-1)!}2 通り
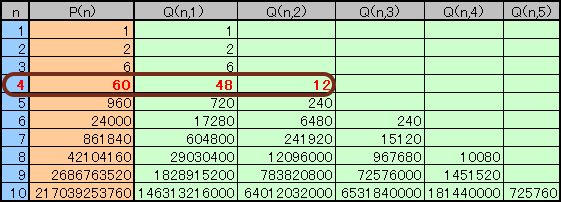
と求まります。なお、n=1のときP(1)=1なので、これを加えてn=1〜10までを計算すると、
下表のようになります。
(追補)本問の数列がオンライン整数列大辞典に登録されました。
直接のリンク先はこちらです。
(参考)n→∞のとき、P(n)/{(n-1)!}2→1.59063685463656
P(n)/{(n-1)!}2=ΣQ(n,k)/{(n-1)!}2の第k項は、
Q(n,k)/{(n-1)!}2
=n!/{(n-2k)!×(2k)!}×(2k)!/k×{(n-k-1)!}2/{(k-1)!}2
=1/{k!×(k-1)!}×[n×(n-1)×・・・×(n-2k+1)/{(n-1)×(n-2)×・・・×(n-k)}2]
となり、
後半部分は、分母、分子とも2k個の積なので、それぞれn2kで割って、
1×(1-1/n)×・・・×{1-(2k-1)/n}/{(1-1/n)×(1-2/n)×・・・×(1-k/n)}2
となるので、n→∞のとき、1に収束。従って、
Q(n,k)/{(n-1)!}2→1/{k!×(k-1)!}よって、
P(n)/{(n-1)!}2=Σ(k=1..∞)1/{k!×(k-1)!}実際に計算すると、
k=1〜11の和=1.59063685463733
・・・
k=1〜15の和=1.59063685463733
ただし、Q(n,k)/{(n-1)!}2自身の収束は、かなり遅く、
n=10のとき、1.6482087743
n=1000のとき、1.5913250049
n=100000のとき、1.5906437440
n=10000000のとき、1.5906368615