第３８１問の解答

問題［空間図形（整数の性質）］

一辺の長さが１cmの白い立方体Ａがたくさんあります。この立方体を積み上げて、一辺の長さがアcmの立方体Ｂを作ります。

立方体Ｂの６つの面のうち、イ面だけをペンキで赤く塗ってからバラバラにしたところ、ペンキが塗られていない立方体Ａは全部で１２００個あったそうです。

ア、イはいくつでしょうか？

解答例１

あ～く＠旧Ｎさん、Taroさん、CRYING DOLPHIN さん、DrKさん、クララさん、中村明海さん、M.Hossieさん、ほげさん、有無相生さん、きょろ文さん、小西孝一さん、シンクロさん、nyamoさん、 他多数

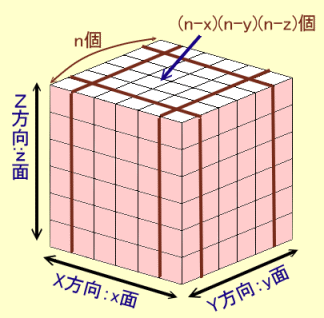
立方体Bの１辺の長さをncmとします。

参考図１

X、Y、Z方向にそれぞれ２面ずつありますが、そのうちx、y、z面にペンキを塗るものとします。
（０≦x、y、z≦２）

このとき、ペンキが塗られないで残るのは、辺の長さが（n-x）、（n-y）および（n-z）cmの直方体となり、この中には立方体Aが（n-x）（n-y）（n-z）個だけ含まれています。

従って、
　（n-x）（n-y）（n-z）＝１２００　・・・　（１）
でなければなりません。

１２００＝１２×１０×１０だから、（１）を満たすものとして、
　n＝１２、（x、y、z）＝（０、２、２）
が考えられます。

このとき、ペンキを塗った面は、
　x＋y＋z＝４面
となります。

さて、これ以外に条件（１）を満たすものがあるでしょうか？
n1＝n-x、n2＝n-y、n3＝n-zとおいて考えてみましょう。

簡単にするため、n1≧n2≧n3とすると、条件（１）は、
　n1×n2×n3＝１２００（ただし、n≧n1≧n2≧n3≧n-2）　・・・　（２）
と書き換えることができます。

（２）より、
　n3≧n1×n2×n3＝１２００≧（n-2）3　・・・　（３）
となります。

ところが、
　１１3＝１３３１＞１２００＞１０3＝１０００
なので、（３）を満たすのは、n＝１２、またはn＝１１に限られます。

（Ⅰ）n＝１２のとき
（２）より、１２≧n1≧n2≧n3≧１０となりますが、
１１は１２００の約数ではないので、n1、n2、n3は１２または１０となります。

n1＝n2＝n3＝１０とすると、n1×n2×n3＝１０3＝１０００となり不適、
よって、いずれか１個は１２でなければなりません。
従って、３個のうち最大のn1が１２と決まります。

よって、n2×n3＝１２００÷１２＝１００となり、n2＝n3＝１０と決まります。

（Ⅱ）n＝１１のとき
（２）より、１１≧n1≧n2≧n3≧９となりますが、
１１は１２００の約数ではないので、１０≧n1≧n2≧n3≧９となり、
従って、１２００＞１０3＝１０００≧n1×n2×n3となり不適です。

以上から、題意を満たすものは、
　n＝１２、n1＝１２、n2＝n3＝１０
に限ることが分かります。

答：　ア：１２cm、イ：４面

以上

解答例２

ミミズクはくず耳さん、すてっぷさん、オモシロ※※館館長「影」さん、他

解答例１で（n-x）（n-y）（n-z）の組み合わせは、x、y、zの３個について、０、１、２から重複を許して選ぶ重複組み合わせ3Ｈ3＝3+3-1Ｃ3＝１０通りあります。

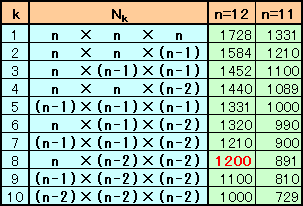
解答例１同様、n＝１２、またはn＝１１に限られることが分かるので、それぞれについて１０組の積の値を計算してみます。

図２
参考図２

すると、積が１２００となるのは、
　n＝１２、積＝n×(n-2)×(n-2)＝ １２×１０×１０
のみであることが分かります。

解答例３

DrKさん、ほげさん、小学名探偵さん、他

　

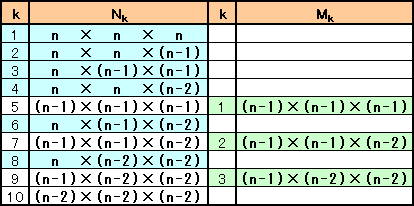
ここでは、一般的に与えられた整数Nが、因数間の差が２以下の３つの整数の積で表されるとき、その表し方は一通りしかないことを背理法で証明してみましょう。

　Ｎ＝n1×n2×n3＝Ｍ＝m1×m2×m3
（ただし、n1≧n2≧n3、n1－n3≦２、m1≧m2≧m3、m1－m3≦２、およびn1≧m1）
と２通りに表されたとします。

まず、解答例２の図２で、n≧３のとき、常にＮ1＞Ｎ2＞Ｎ3＞・・・＞Ｎ10となることを確認します。 　・・・　（＊＊）

・Ｎ1＞Ｎ2＞Ｎ3　・・・　各因数の大小関係より明らか
・Ｎ3＞Ｎ4　　　・・・　(n－１)×(n－１)＞n×(n－２)だから
・Ｎ4＞Ｎ5　　　・・・　Ｎ4－Ｎ5＝（n3－2n2）－（n3－3n2＋3n－1）＝n×(n－３)＋１＞０
・Ｎ5＞Ｎ6　　　・・・　(n－１)×(n－１)＞n×(n－２)だから
・Ｎ6＞Ｎ7　　　・・・　各因数の大小関係より明らか
・Ｎ7＞Ｎ8　　　・・・　(n－１)×(n－１)＞n×(n－２)だから
・Ｎ8＞Ｎ9＞Ｎ10　・・・　各因数の大小関係より明らか

（Ⅰ）n1≧m1＋２のとき
n1＞m1、n2、n3≧n1－２≧m1≧m2、m3より、
　Ｎ＝n1×n2×n3＞m1×m2×m3＝Ｍとなり、不適。

（Ⅱ）n1＝m1のとき
n＝n1＝m1とすると、N、Mは図２のＮ1～Ｎ10のいずれかとなるが、
（＊＊）よりN＝Mならば、（n1、n2、n3）＝（m1、m2、m3）となって、不適。

（Ⅲ）n1＝m1＋１のとき
NはＮ1、Ｎ2、Ｎ3、Ｎ4、Ｎ6、Ｎ8のいずれか、MはM1、M2、M3、M4、M6、M8のいずれかになります。 ところが、M1＝Ｎ5、M2＝Ｎ7、M3＝Ｎ9なので、N＝Mとはなりません。

参考図３

（その他の解法）