第３８２問の解答

問題［整数の性質 （場合の数）］

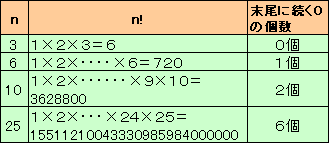問題図 左図のように、１からnまでの整数を全部掛け算すると（n！＝nの階乗）、末尾にいくつか０が続きます。

では、０以上１０００以下の整数の中で、末尾に続く０の個数になることができないものはいくつあるでしょうか。

解答例１

マサルさん、Taroさん、CRYING DOLPHINさん、もありすさん、那由他さん、sugitakukunさん、シンクロさん、拓パパさん、小西孝一さん、ミミズクはくず耳さん、小学名探偵さん、ちこりんさん、M.Hossieさん、ポケモンハルカさん、 他多数

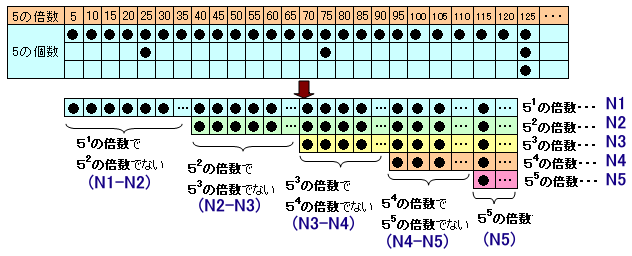
１０＝２×５と素因数分解できますので、n！で末尾に続く０の個数は、n！に含まれる２と５の個数を数えることになりますが、２の個数は５の個数よりもはるかに多いので、５の個数だけ調べればいいことになります。

参考図１

上表より、１から順に整数を掛け合わせていくと、５の倍数が現れるたびに１個ずつ５の個数が増えていきます。
ただし、２５の倍数や１２５の倍数のように５を複数個因数として持つ整数のときは、累計個数として表せない整数が発生します。（５kの倍数のときにk-1個） 　・・・　（１）

このまま地道に数えていくのも一つの方法ですが、いずれにしてもn！にある５の個数（Nとします）が１０００以上となるnをまず調べてみましょう。

参考図２

n！に含まれる５kの倍数の個数をNkとします。
　Nk＝[n/５k]　（ただし、[ｘ]は、ｘの整数部分を表す）
と表されます。

５６＝１５６２５となるので、５5の倍数までを数えればいいことが分かります。
上図で横方向に数えていけば、
　N＝N1＋N2＋N3＋N4＋N5
となります。

これは、縦方向に数えていくと、
　N＝（N1−N2）×１＋（N2−N3）×２＋（N3−N4）×３＋（N4−N5）×４＋N５×５
　　＝N1＋N2＋N3＋N4＋N5
となることからも分かります。

Nk≒n/５k（誤差は１より小）なので、
　N≒n/５1＋n/５2＋n/５3＋n/５4＋n/５5＋
　　≒n/５1×１／（１−１/５）
　　＝n/４

よって、N≧１０００となるのは、n≒１０００×４＝４０００と分かります。
さて、n＝４０００のとき、
　N1＝[4000/5]＝８００、N2＝[4000/25]＝１６０、N3＝[4000/125]＝３２、
　N4＝[4000/625]＝６、N3＝[4000/3125]＝１　
より、N＝８００＋１６０＋３２＋６＋１＝９９９個

また、n＝４００５のとき、
　N1＝[4005/5]＝８０1、N2＝[4005/25]＝１６０、N3＝[4005/125]＝３２、
　N4＝[4005/625]＝６、N3＝[4005/3125]＝１　
より、N＝８０１＋１６０＋３２＋６＋１＝１０００個となります。

さて、（１）より、１０００までの整数で５の累計個数とならないものの個数をｎ'とすると、
　n'＝（N2−N3）×１＋（N3−N4）×２＋（N4−N5）×３＋N５×４
　　＝N2＋N3＋N4＋N5
　　＝１６０＋３２＋６＋１
　　＝１９９個
と求まります。

これは、１０００までに現れる５の累計個数のパターンが、N1＝８０１個ということから、
　n'＝N−N1＝１０００−８０１＝１９９個
とも計算できます。

答：　１９９個

以上

（その他の解法）