第383問の解答
問題[平面図形]
|
|
|
|
|
|
|
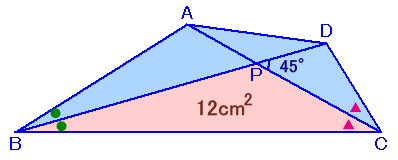 |
左図のような四角形ABCDがあります。 ACは∠Cの、BDは∠Bの二等分線になっていました。また、対角線の交点をPとすると、∠DPC=45度となりました。 では、△PBCの面積が12cm2であるとき、四角形ABCDの面積を求めてください。 |
|
|
|
|
|
|
解答例1
トトロ@Nさん、CRYING DOLPHINさん、あ〜く@旧Nさん、きょろ文さん、もありす55さん、Taroさん、中村明海さん、すてっぷさん、小西孝一さん、hiroさん、ねこやんさん、omegaさん、ちこりんさん、ポケモンハルカさん、 他多数
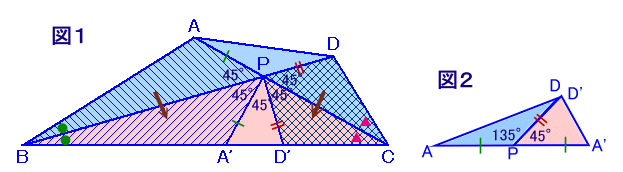
BPを軸にして△ABPを折り返したものを△A'BP、およびPCを軸にして△DCPを折り返したものを△D'CPとします。
まず、△ABP=△A'BPおよび△DCP=△D'CPが成り立ちます。
また、∠A'PB=∠APB=45°、∠D'PC=∠DPC=45°より、
∠A'P'D=180−45×3=45°さらに、∠APD=180−45=135°で、DP=D'Pより、
△DAPと△D'PA'を図2のように合わせればA、P、A'は一直線上に並び、DとD'は一致します。しかも、AP=A'Pより、△DAPと△DP'A'は底辺の長さが等しく、高さが共通なので面積は等しい。
よって、
△ABP+△DAP+△DPC
=△A'BP+△DP'A'+△D'PC
=△PBC従って、
四角形ABCD
=(△ABP+△DAP+△DPC)+△PBC
=△PBC×2
=24cm2
と求まります。答: 24cm2
以上
解答例2
すてっぷさん、RDさん、 他
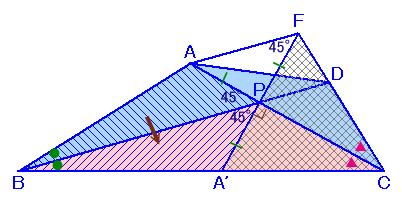
BC上にA'をBA'=BAとなるようにとり、A'PおよびCDの延長が交わる点をFとします。
∠APB=∠A'PB=45°より、
∠A'PC=180−45×2=90°となります。よって、△CA'Pと△CFPに関して、
CPが共通で、∠A'CP=∠FCPおよび∠CPA'=∠CPF=90°だから合同。よって、FP=A'P=AP、かつ∠APF=180−45×2=90°より、
△PFAは直角二等辺三角形となります。従って、∠AFP=45°となり、∠AFP=∠BPA'=45°より、AFとBDは平行となります。
よって、△APDと△FPDは、底辺PDが共通で高さが等しいので面積が等しい。従って、
△ABP+△DAP+△DPC
=△A'BP+△FPD+△DPC
=△A'BP+△APC
=△A'BP+△A'PC
=△PBC以下、解答例1と同様。
(その他の解法)
- 三角関数を駆使して解く ・・・ M.Hossieさん、 有無相生さん、他