第３８４問の解答

問題［平面図形］

問題図

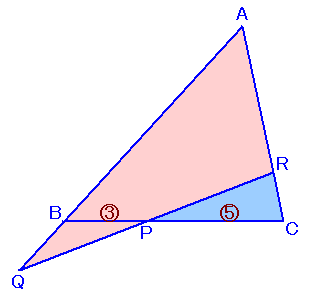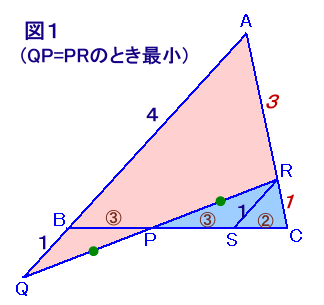
左図のような、面積が２４cm2の△ＡＢＣの辺ＢＣ上に点Ｐを、ＢＰ：ＰＣ＝３：５になるようにとります。さらに、辺ＡＢの延長上に点Ｑを、辺ＡＣ上に点Ｒをとり、線分ＱＲが点Ｐを通るようにして、△ＡＱＲを作ります。

では、△ＡＱＲの面積が最も小さくなるようにＱ、Ｒをとるとき、△ＡＱＲの面積は何cm2になるかを求めてください。

解答例１

はなうさん、シンクロさん、あ〜く＠旧Ｎさん、ｎさん、ねこやんさん、遠い山のぽきょぽんさん、ろろさん、小学名探偵さん、まるケンさん、ばち丸さん、きょろ文さん、 他多数

あとで証明しますが、△AQRの面積が最小となるのはQP＝PRとなるときです。
まず、このときの最小値を求めましょう。

参考図１

（△AQRの最小値）

点Rを通って辺AQと平行な直線と辺BCの交点をSとします。

△BQPと△SRPに関して、QP＝RP、∠BPQ＝∠SPR（対頂角）、∠BPQ＝∠SPR（錯角）より、
１辺と両端の角が等しいので合同。

従って、BQ＝SR、BP＝SP、
BP：PC＝３：５より、BS：SC＝６：２＝３：１

RSとABは平行より、△CRSと△CABは相似、
よって、
　CR：RA＝CS：SB＝１：３　・・・　（１）

また、
　RS：AB＝CS：CB＝１：４
RS＝BQより、
　AB：BQ＝４：１　・・・　（１）

従って、（１）、（２）より、
　△AQR＝△ABC×AQ/AB×AR/AC
　　　＝２４×５/４×３/４
　　　＝４５/２cm2
 と求まります。

（QP＝PRのときに△AQRが最小であること）

参考図２

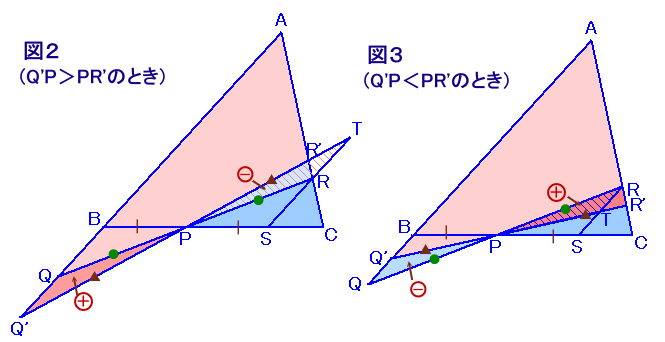
SRとQRの交点をTとします。
△BQ'Pと△STPに関して、BP＝PS、∠BPQ'＝∠SPT（対頂角）、∠BQ'P＝∠STP（錯角）より、
１辺と両端の角が等しいので合同。

  • Q'P＞PR'のとき

△QQ'P＝△BQ'P−△BQP、△RTP＝△STP−△SRPより、
△QQ'P＝△RTP

△AQ'R'＝△AQR＋△QQ'P−△RR'P
　　＝△AQR＋△QQ'P−（△RTP−△TR'R）
　　＝△AQR＋△TR'R＞△AQR　・・・　（３）

  • Q'P＞PR'のとき

△QQ'P＝△BQP−△BQ'P、△RTP＝△SRP−△STPより、
△QQ'P＝△RTP

△AQ'R'＝△AQR−△QQ'P＋△RR'P
　　＝△AQR−△QQ'P＋（△RTP＋△TR'R）
　　＝△AQR＋△TR'R＞△AQR　・・・　（４）

（３）、（４）より、
　

QP＝PRのとき△AQRが最小であることが分かります。

答：　４５/２cm2

以上

解答例２

M.Hossieさん、 那由他さん、小西孝一さん、ゴンともさん、とまぴょんさん、kasamaさん、他

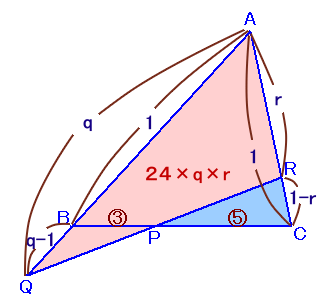
q＝AQ/AB、r＝AR/ACとします。（q＞1）

参考図３

△ABCと直線QRに関してメネラウスの定理より、
　AQ/QB×BP/PC×CR/RA＝１
　ｑ/（ｑ−１）×３/５×（１−ｒ）/ｒ＝１

よって、
　ｒ＝３ｑ/（8ｑ−５）

従って、△AQRの面積をSとおくと、
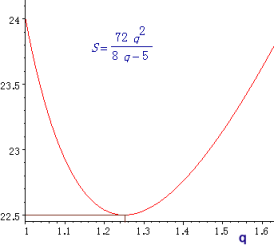
　S＝２４×ｑ×ｒ
　　＝７２×ｑ2/（８ｑ−５）

ここで、ｔ＝８ｑ−５とおくと、ｑ＝（ｔ＋５）/８より、
　S＝７２/８2×（ｔ＋５）2/ｔ
　　＝９/８×（ｔ＋１０＋２５/ｔ）
　　≧９/８×（２×√（ｔ×２５/ｔ)＋１０）　・・・　（１）
　　＝９/８×２０
　　＝４５/２cm2

（１）は、（ａ+ｂ）/２≧√（ab）（算術平均≧幾何平均）より導かれ、
等号はｔ＝２５/ｔ、すなわちｔ＝５の時に成り立つ。

このとき、ｑ＝５/４、ｒ＝３/４となる。

(参考)

参考図４

（その他の解法）