第385問の解答
問題[平面図形]
|
|
|
|
|
|
|
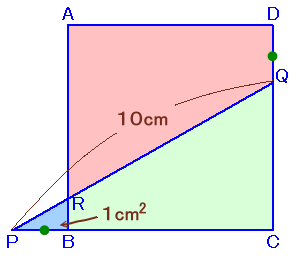 |
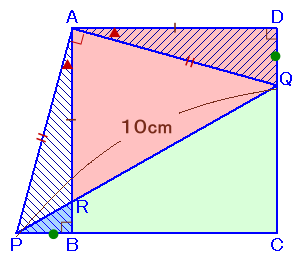
左図のような、正方形ABCDがあります。 いま、CBの延長上に点Pを、辺CD上に点Qを、BP=DQとなるようにとったところ、PQ=10cmとなりました。また、PQとABの交点をRとすると、△PBRの面積は1cm2となったそうです。 このとき、四角形ARQDの面積を求めてください。 |
|
|
|
|
|
|
解答例1
マサルさん、CRYING DOLPHINさん、ちずさん、はんたろうさん、M.Hossieさん、neoさん、とまぴょんさん、浮浪さん、大岡 敏幸さん、 他多数
APとAQを結んで△APQに着目してみましょう。
△APBと△AQDについて、
PB=QD、AB=AD、∠ABP=∠ADQ=90°より、二辺挟角が等しいので合同。よって、AP=AD、∠PAB=∠QAD。
従って、∠QAP=∠PAR+∠PAB=∠PAR+∠QAD=∠BAD=90°。
よって、△APQは直角二等辺三角形となります。△APQの斜辺の長さは、PQ=10cmなので、
△APQ=5×5=25cm2。よって、
四角形ARQD
=△ARQ+△AQD
=△ARQ+△APB
=△ARQ+△APR+△PBR
=△APQ+△PBR
=25+1=26cm2
と求まります。答: 26cm2
以上
解答例2
はなうさん、あ〜く@旧Nさん、遠い山のぽきょぽんさん、takaisaさん、ねこやんさん、ちこりんさん、nさん、きょろ文さん、くりこめっちさん、他
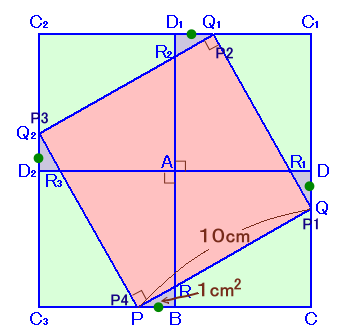
問題の図形を90度ずつ回転しながら4個くっつけてみます。
PB=QDより、P1とQ、P2とQ1、P3とQ2、およびP4とPはそれぞれ一致します。
よって、R1、R2、R3は、それぞれQQ1とDA、Q1Q2とD1A、およびQ2PとD2Aの交点と一致します。
従って、四角形PQQ1Q2=四角形ARQR1×4となります。
さて、QQ1、Q1Q2、およびQ2Pは、PQが90度ずつ回転したものだから、辺の長さはそれぞれ等しく、
また、∠PQQ1=∠QQ1Q2=∠Q1Q2P=∠Q2PQ=90度となることから、
四角形PQQ1Q2は正方形と分かります。よって、正方形PQQ1Q2=102=100cm2。
従って、
四角形ARQD
=四角形ARQR1+△QDR1
=正方形PQQ1Q2×1/4+△PBR=
=100×1/4+1=26cm2
と求まります。
解答例3
信三さん、M.Hossieさん、あささん、他
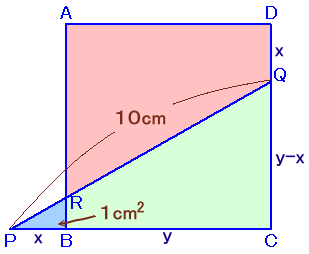
x=PB、y=BCとします。
題意より、DQ=x、QC=DC−DQ=y-xとなります。
また、△QPCは直角三角形だからピタゴラスの定理より、
PQ2=PC2+QC2よって、
102=(x+y)2+(y−x)2従って、x2+y2=50となります。
よって、
四角形ARQD
=正方形ABCD−四角形RBCQ
=正方形ABCD−(△QPC−△PBR)
=y2−1/2×(x+y)(y−x)+1
=1/2×(x2+y2)+1
=1/2×50+1=26cm2
と求まります。
(その他の解法)
- プログラム等で方程式を解いて求める ・・・ Taroさん、なかさん、ハラギャーテイさん、 他
x2+y2=50、1/2×(y2-x2)・{x/(x+y)}2=1より、(y,x)=(5.47,4.48),(6.82,1.88)を得ます。