第387問の別解
解答例1(小学名探偵さん)
ちょうど8歩目に元の位置に戻るような歩き方を帰巣型と呼び、8歩目まで(一般的には2n歩目)に一度も元の位置を経ない歩き方を家出型と呼ぶことにします。
基本的性質やルールは次の通りです。
最初に右に歩く場合に限定して考えますが、最初に左へ歩く場合も全く同様です。
経路図では、右へ歩くのを横方向(左→右)、左に歩くのを縦方向(下→上)で描くことにし、
最初の位置Aを原点(0、0)とすると右に合計x歩、左に合計y歩歩いた位置は(x、y)とあらわすことができます。(1)ある前向きの帰巣型経路Kを前向きの家出型経路Iに変換する場合:
この場合、原点から帰巣型経路Kのゴールに向かって辿っていって、順次、経路Iの各部を決めていくのがよいようです。
最初の一歩はどちらも同じです。
(0,0)から(1,0)へ進む
経路Kがある格子点で右向きから上向きにターンするとき、
経路Iはそこから右向きに進ませます。
経路Kがある格子点で上向きから右向きにターンするとき、
経路Iは上向きに進ませます。
経路Kが直進を続け経路Iと出会わない限り経路Iも直進させます。
経路Kと経路Iが再び出会ったとき、
経路Kがそこで右向きから上向きにターンすれば、ルール2同様を経路Iは右向きに進ませます。
経路Kがそこでターンせず直進するときは、次に経路Kがターンするところまで
経路Iは経路Kと同じパスを進ませます。
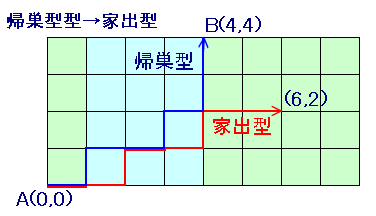
例:帰巣型経路が
(0,0)、(1,0)、(1,1)、(2,1)、(3,1)、(3,2)、(4,2)、ゴール(4,4)の場合、
(0,0)、(1,0)、(2,0)、(2,1)、(3,1)、(4,1)、(4,2)、ゴール(6,2)
の家出型の経路に変換されます。
(2)ある前向きの家出型経路Iを前向きの帰巣型経路Kに変換する場合:
この場合、家出型経路Iのゴールから原点に向かってさかのぼっていって、
順次、経路Kの各部を決めていくのがよいようです。
最初の一歩は、進む方向を異なるようにとります。
すなわち、経路Iが左なら経路Kは下向き、経路Iが下向きなら経路Kは左向き。
経路Iがある格子点で左向きから下向きにターンするとき、
経路Iはそこから左向きに進ませます。
経路Iがある格子点で下向きから左向きにターンするとき、
経路Kは下向きに進ませます。
経路Iが直進を続け経路Kと出会わない限り経路Kも直進させます。
経路Iと経路Kが出会ったならば、
経路Iがそこで左向きから下向きにターンすればルール2同様経路Kを左向きに 進ませます。
そこでターンしなければ次に経路Iがターンするところまで
経路Kは経路Iと同じパスを進ませます。
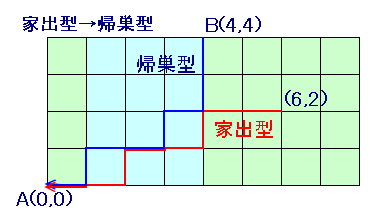
例:さかのぼる方向で見て、家出型の経路が
(6,2)、(4,2)、(4,1)、(3,1)、(2,1)、(2,0)、(1,0)、(0,0)の場合、
(4,4)、(4,2)、(3,2)、(3,1)、(2,1)、(1,1)、(1,0)、(0,0)に
変換された帰巣型経路が出来ます。
さて、上記ルールで変換するとき、
帰巣型経路を変換したものは、必ず家出型経路になる
家出型経路を変換したものは、必ず帰巣型経路になる
異なる帰巣型経路の変換経路は異なる家出型経路に
異なる家出型経路の変換経路は異なる帰巣型経路になることを示すことができれば、帰巣型経路の個数と家出型経路の個数は等しいことが証明できます。
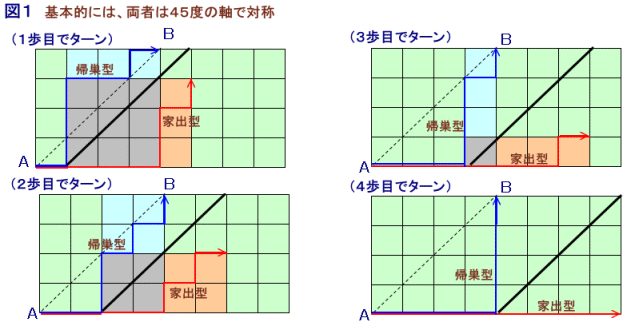
3.は変換ルールがちょうど互いに逆変換になっているので1.および2.が示されれば明らかです。1.帰巣型経路を変換したものは、必ず家出型経路になること
ターン後は、変換後の経路は元の帰巣型経路と45度の線を軸にして対称となっている。
この対称軸は、対角線ABより右にあるので、両者が再び出会うことがなければ、
帰巣型経路は対称軸より上側、変換後経路は対称軸より右にあるので、
変換後経路は対角線ABと交わることはない。また歩数も帰巣型と同じなので、変換後経路は家出型となります。
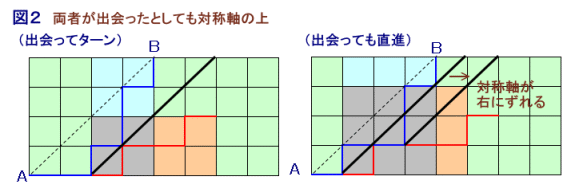
もし、両者が出会ったとしても対称軸上であり、
出会った地点で帰巣型がターンすれば、以降も対称軸より上側にあり続けます。また、帰巣型がターンせずに直進すると、対称軸がターンする地点まで右にずれていきます。
どこかでターンしないと帰巣型はBにたどり着けないので、必ずどこかでターンし、以降は対称軸より上側にあり続けます。従って、変換後経路は対角線ABと交わることはありません。
2.家出型経路を変換したものは、必ず帰巣型経路になること
ほぼ1.の場合の議論を逆にすることになります。
手抜きして1.の図1、図2で説明することにしますが、経路を逆にたどって下さい。両者とも地点(1、0)を通るので、必ずどこかで出会います。
両者が出会うまでは、変換後経路は家出型経路と45度の線を軸にして対称のなので、
変換後経路は地点Bと対称軸の下端とを対角点にする長方形の中(外周を含む)を進みます。この長方形は、ABを対角とする長方形に含まれています。また、両者が最初に出会うのが対称軸の下端なら、それ以降の変換後経路は家出型経路と同じくA地点まで左向きに直進するので、結局変換後経路はABを対角とする長方形内を進むことになるので、帰巣型経路になります。
もし、両者が対称軸の下端以外で出会ったとしても、対称軸の途中であり、
家出型経路が出会った地点でターンすれば、以降も対称軸は変わりません。家出型経路がターンせずに直進すると、再度ターンするまで(家出型はAを通る水平軸を通るので、どこかでターンします)変換後経路も家出型と同じ経路をたどります。
家出型経路がターンすると、対称軸はターン地点を通る45度の線にずれますが、ずれたとしても(1、0)を通る45度線よりは右側(重なる場合を含む)にあります。
変換後経路は、ずれた対称軸の上側にあるので、依然として対称軸の下端とターン地点を対角点とする長方形内を進みますが、この長方形もABを対角とする長方形に含まれます。
従って、変換後経路は、必ずABを対角とする長方形を進むので、帰巣型経路になります。
以上で、1.、2.、3.が示されましたので、帰巣型経路の個数と家出型経路の個数が等しいことが証明できま した。