第391問の解答
問題[平面図形]
|
|
|
|
|
|
|
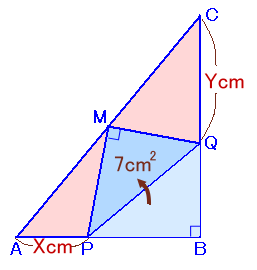 |
左図のような直角三角形ABCがあります。 いま、ACの中点Mに頂点Bが重なるように折ったところ、折り目が図の線分PQとなりました。 また、
のとき、APの長さとCQの長さの積(XとYの積)を求めてください。 |
|
|
|
|
|
|
解答例1
takaisaさん、なかさん、トトロ@Nさん、kasamaさん、きょろ文さん、hiroさん、龍洋里さん、他
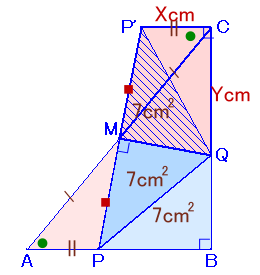
Mを中心に△MAPを180度回転したものを△MCP’とします。
△MCP’と△MAPは合同だから、
MP’=MP、CP’=AP=Xcm、∠MCP’=∠MAPすると、P’CとABは平行となり、∠PC’B=∠CBA=90度。
また、△P’MQと△PMQについて、P’M=PM、MQは共通、∠P’MQ=∠PMQ=90度より、
二辺挟角が等しいので合同、
よって、△P’MQ=△PMQ=7cm2。従って、
△P’QC=1/2・X・Y
=(△MCP’+△CMQ)−△P’MQ
=(△MCP+△CMQ)−△PMQ
=13−7
=6cm2よって、
X・Y=6×2=12
と求まります。答: 12
以上
解答例2
拓パパさん、Яunnerさん、牝牛さん、他
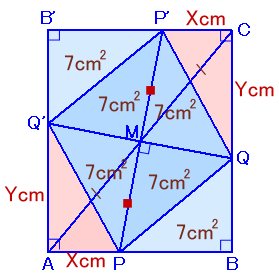
解答例1とほぼ同じですが、△ABCを180度回転したものを△CB’Aとし、
点P、Qに対応する点をP’、Q’とします。
すると、四角形B’ABCは長方形になります。
長方形B’ABC=△ABC×2=(13+7×2)×2=54cm2。
X・Y
=長方形B’ABC−△MPQ×6
=54−7×6
=12
と求まります。
解答例3
ゴンともさん、takachanさん、やくわさん、M.Hossieさん、とまぴょんさん、大岡 敏幸さん、やくわさん、他
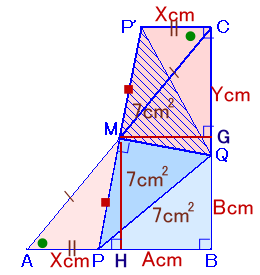
解答例1の図で、MからABおよびBCに下ろした垂線の足をHおよびGとします。
また、PB=Acm、QB=Bcmとおきます。
△ABC=1/2・(X+A)・(Y+B)=13+7×2より、
X・Y+B・X+A・Y+A・B=54 ・・・ (1)△MAP+△CMQ=1/2・X・(Y+B)・1/2+1/2・X・(Y+B)・1/2=13cm2より、
2・X・Y+B・X+A・Y=52 ・・・ (2)△QPB=1/2・A・B=7より、
A・B=14 ・・・ (3)(1)−(3)より、
X・Y+B・X+A・Y=40 ・・・ (4)(2)−(4)より、
X・Y=12 ・・・ (5)
と求まります。
(参考)具体的なX、Y、X、Bの値を求める方法。
(4)、(5)より、
B・X+A・Y=30 ・・・ (6)
(3)、(5)より、
(B・X)・(A・Y)=168 ・・・(7)(6)、(7)より、B・XとA・Yは、
x2−30x+168=0
の2根となります。よって、これらをα、βとおくと、
A=α/Y、B=β/X ・・・ (8)また、P’Q2=PQ2より、
X2+Y2=A2+B2(3)、(5)および(8)より、
X2+(12/X)2=(αX)2+(β/X)2これは、X2に関する2次方程式となりますので、Xが得られます。
以下省略。
(その他の解法)
- 三角関数で解く ・・・ とまぴょんさん、 他