第392問の解答
問題[場合の数]
|
|
|
|
|
|
|
 |
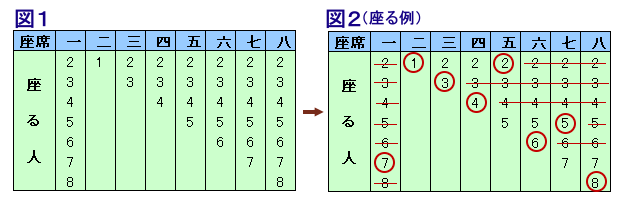
一郎〜八郎までの8人兄弟が円卓で食事をすることになりました。それぞれの座席は左図のように決められています。 ある日、一郎が間違えて右隣の二郎の座席に座ってしまいました。そこで、その後に座席につく兄弟は、
ことにしました。 このとき、8人の座り方は何通り考えられるでしょうか。 |
|
|
|
|
|
|
解答例1
遠い山のぽきょぽんさん、シンクロさん、目崎達也さん、小学名探偵さん、ゴンともさん、スモークマンさん、他
どの人も、自席または自席より右にずれていった席に座るので、
各座席に座る可能性のある人は、次の通り。
二郎の席 ・・・ 一郎で確定
三郎の席 ・・・ 二郎か三郎
四郎の席 ・・・ 二郎か三郎か四郎
五郎の席 ・・・ 二郎か三郎か四郎か五郎
六郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎
七郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎か七郎
八郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎か七郎か八郎
一郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎か七郎か八郎
そこで、三郎の席から順に座る人を決めていくと、
三郎の席 ・・・ 二郎か三郎 → 2通り
四郎の席 ・・・ 二郎か三郎か四郎のうち三郎の席に座った人を除く → 2通り
五郎の席 ・・・ 二郎か三郎か四郎か五郎のうち既に座った2人を除く → 2通り
六郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎のうち既に座った3人を除く → 2通り
七郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎か七郎のうち既に座った4人を除く → 2通り
八郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎か七郎か八郎のうち既に座った5人を除く → 2通り
一郎の席 ・・・ 二郎か三郎か四郎か五郎か六郎か七郎か八郎のうち残った一人 → 1通り
従って、合計=26=64通りになります。
答: 64通り
以上
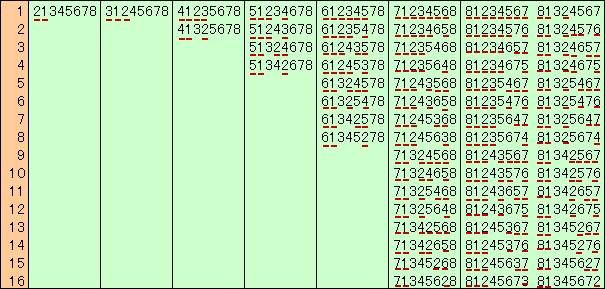
(参考)なかさんによる座席表を紹介しておきます。
なお下線があるのは、自分の座席に座れなかった人です。
解答例2
はなうさん、小学名探偵さん、他
一郎と二郎が自席に座れないのは確定しています。
それ以外の6人のうちk人(k=0から6)が自席に座れないとしたとき、
一郎、二郎とこのK人は、自席に座った人の座席(6−k)個を除く、(k+2)個の空席に年上から順に座っていくことになります。(一郎は一番最初で確定)
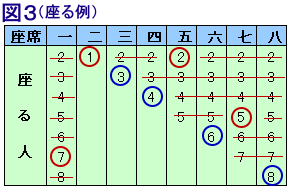
このことを五郎と七郎が自席に座れない場合で考えます。(k=2)
もし五郎か七郎が二郎より前に座るとすると、自席が空いているので座れることになり不適。
従って、二郎が最初に座ります。その座席は、このでは、五郎の座席になります。次に、五郎と七郎で、七郎が先に座ると、七郎が自席に座れることになり不適、
よって五郎が先で七郎の席に、七郎は残った一郎の席に座ることになります。他の場合も全く同様に、年上順に座ることが分かります。
従って、自席に座れない人を決めれば、その座り方は一意的に決まります。よって、
自席に座れない人が0人 ・・・ 三郎から八郎の6人から0人を選ぶ6C0=1通り
自席に座れない人が1人 ・・・ 三郎から八郎の6人から1人を選ぶ6C1=6通り
自席に座れない人が2人 ・・・ 三郎から八郎の6人から2人を選ぶ6C2=15通り
自席に座れない人が3人 ・・・ 三郎から八郎の6人から3人を選ぶ6C3=20通り
自席に座れない人が4人 ・・・ 三郎から八郎の6人から4人を選ぶ6C4=15通り
自席に座れない人が5人 ・・・ 三郎から八郎の6人から5人を選ぶ6C5=6通り
自席に座れない人が6人 ・・・ 三郎から八郎の6人から0人を選ぶ6C6=1通り
合計=64通りとなります。
なおこの計算は、
6C0+6C1+6C2+6C3+6C4+6C5+6C6=(1+1)6=64
でも求まります。
解答例3
らんき〜さん、遠い山のぽきょぽんさん、小西孝一さん、takachanさん、小学名探偵さん、他
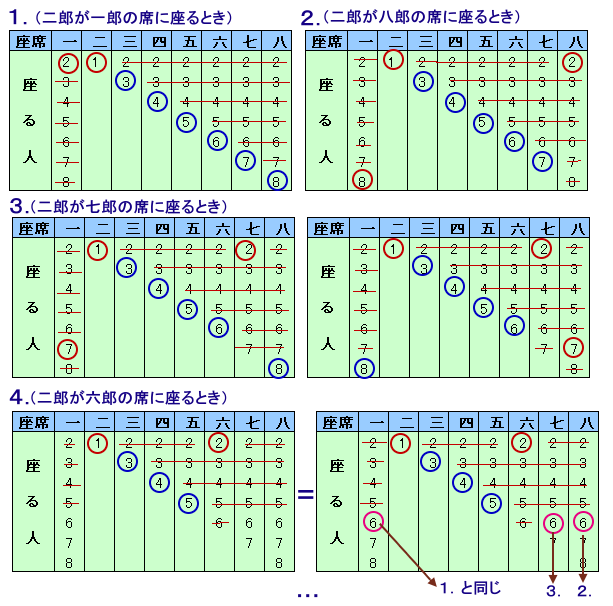
二郎が座る位置で考えます。
一郎の席に座るとき:
三郎の席には、二郎か三郎が座るところ二郎は既に座っているので三郎が座ることに
四郎の席には、二郎か三郎か四郎が座るところ二郎と三郎は既に座っているので四郎が座ることに
以下、同様に五郎から八郎まで自席に座る ・・・ 1通り
八郎の席に座るとき:
1.と同様に三郎から七郎まで自席に座り、残った八郎が一郎の席に座る ・・・ 1通り
七郎の席に座るとき:
同様に三郎から六郎まで自席に座る
七郎が座るのが一郎の座席のとき ・・・ 1.と同じ1通り
七郎が座るのが八郎の座席のとき ・・・ 2.と同じ1通り 計2通り
六郎の席に座るとき:
同様に三郎から五郎まで自席に座る
六郎が座るのが一郎の座席のとき ・・・ 1.と同じ1通り
六郎が座るのが八郎の座席のとき ・・・ 2.と同じ1通り
六郎が座るのが八郎の座席のとき ・・・ 3.と同じ1通り 計4通り
・・・合計=1+1+2+4+8+16+32=64通り
解答例4
小学名探偵さん、トトロ@Nさん、大岡 敏幸さん、他
兄弟の人数がn人のときの座り方をAn(ただし、n≧2)として、nに関する漸化式を考えましょう。
Anまで求まったとき、1人増えて(n+1)人のときを求めます。
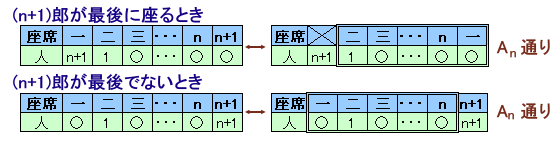
増えた(n+1)郎が最後に座るとき:
(n+1)郎は最後に残った一郎の席に座ることになります。
残りのn人の座り方は、(n+1)郎の席を一郎の席と見なすと、ちょうどn人のときの座り方と同じ・・・An通り
増えた(n+1)郎が最後ではないとき:
(n+1)郎の後に1人以上残っているので、自席が埋まっていることはありません。
従って、(n+1)郎は自席に座ることになります。
残りのn人の座り方は、(n+1)郎の席を無視すると、ちょうどn人のときの座り方と同じ・・・An通りよって、
An+1=An×2
が成り立ちます。A2=1だから、
An=A2×2n-2=2n-2通りとくに本問では、n=8として、
An=26=64通り
(その他の解法)
- 二郎が何番目に席に着くかで着目 ・・・ DrKさん、他
6C0+6C1+6C2+6C3+6C4+6C5+6C6=64通り
- 最後に座る人で場合分けし漸化式的に考える ・・・ ちこりんさん、M.Hossieさん、他
n郎が最後の時をBn通りとすると、B2=1、Bn+1=B2+B3+・・+Bnが成り立つ→Bn=2n-2通り
- プログラム(C、EXCEL)で解く ・・・ naruさん、??? さん、他