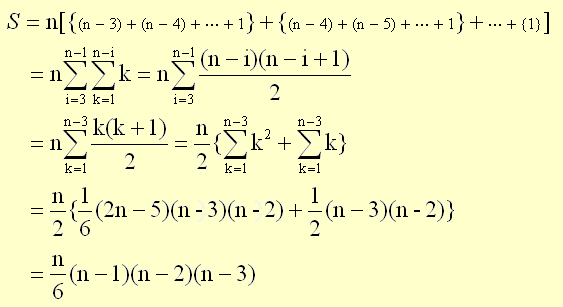第３９４問の解答

問題［場合の数］

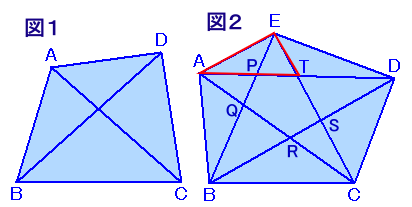図１のように、凸型四角形に対角線を全て引くとき、もとの四角形の頂点を２個含む三角形は４個できますね。

では、凸型７角形に対角線を全て引くとき、もとの７角形の頂点をちょうど２個含む三角形は何個できるでしょうか。

ただし、例えば凸型５角形の場合（図２参照）、頂点Ａと頂点Ｅを含む三角形には、図の△ＡＴＥのようなものも含むものとします。（ちなみに頂点Ａと頂点Ｅを含む三角形は、△ＡＰＥ、△ＡＴＥ、△ＡＱＥの３つですね。）

解答例１

はなうさん、トトロ＠Ｎさん、あ～く＠旧Nさん、ゴンともさん、ミミズクはくず耳さん、小西孝一さん、スモークマンさん、きょろ文さん、　Taroさん、圭太さん、ちこりんさん、他

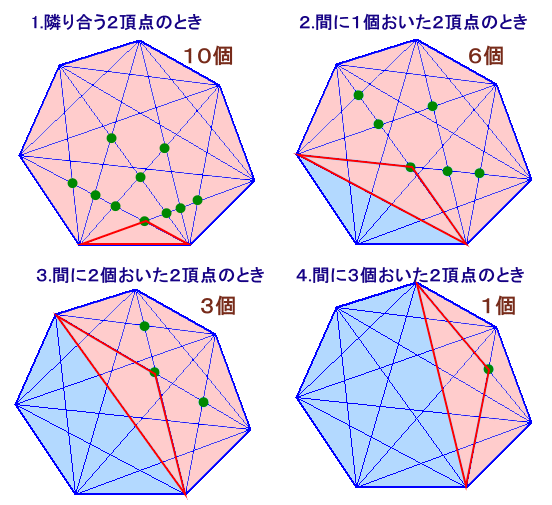
２個の頂点の位置関係で場合分けします。

２頂点が隣り合うとき　：　残る頂点は、この２頂点を含む２本の対角線の交点
　・・・　４＋３＋２＋１＝１０個

２頂点の間に頂点が１個のとき　：　残る頂点は、この２頂点を含む２本の対角線の交点
　・・・　３＋２＋１＝６個

２頂点の間に頂点が２個のとき　：　残る頂点は、この２頂点を含む２本の対角線の交点
　・・・　２＋１＝３個

２頂点の間に頂点が３個のとき　：　残る頂点は、この２頂点を含む２本の対角線の交点
　・・・　１個

これらの２頂点は、７角形では７個ずつあるから、
　求める三角形の個数＝（１０＋６＋３＋１）×７＝１４０個
と求まります。

答：　１４０個

以上

一般に一般的にｎ角形（ｎ≧４）なら、

解答例２

長野美光さん、はなうさん、とまぴょんさん、takachanさん、　なかさん、他

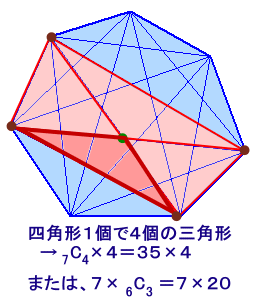
題意を満たす三角形は、７角形の４個の頂点からなる四角形でできるだから、
　₇C₄×４＝３５×４＝１４０個
と求まります。

あるいは、１個の頂点を決めて、残りの２点は、次の頂点、対角線の交点と考えると、
　７×₆C₃＝７×２０＝１４０個
とも求まります。

一般的にｎ角形（ｎ≧４）なら、
　_nC₄×４＝n(n-1)(n-2)(n-3)/6
または、
　ｎ×_n-1C₃＝n(n-1)(n-2)(n-3)/6
となります。

（その他の解法）

0,4,20の数列を考えた　・・・　ハラギャーテイさん、他
　
実際に数えた　・・・　M.Hossieイさん、他


	２個の頂点の位置関係で場合分けします。２頂点が隣り合うとき　：　残る頂点は、この２頂点を含む２本の対角線の交点　・・・　４＋３＋２＋１＝１０個２頂点の間に頂点が１個のとき　：　残る頂点は、この２頂点を含む２本の対角線の交点　・・・　３＋２＋１＝６個２頂点の間に頂点が２個のとき　：　残る頂点は、この２頂点を含む２本の対角線の交点　・・・　２＋１＝３個２頂点の間に頂点が３個のとき　：　残る頂点は、この２頂点を含む２本の対角線の交点　・・・　１個これらの２頂点は、７角形では７個ずつあるから、　求める三角形の個数＝（１０＋６＋３＋１）×７＝１４０個と求まります。答：　１４０個以上一般に一般的にｎ角形（ｎ≧４）なら、


	題意を満たす三角形は、７角形の４個の頂点からなる四角形でできるだから、　₇C₄×４＝３５×４＝１４０個と求まります。あるいは、１個の頂点を決めて、残りの２点は、次の頂点、対角線の交点と考えると、　７×₆C₃＝７×２０＝１４０個とも求まります。一般的にｎ角形（ｎ≧４）なら、　_nC₄×４＝n(n-1)(n-2)(n-3)/6 または、　ｎ×_n-1C₃＝n(n-1)(n-2)(n-3)/6 となります。