第３９５問の解答

問題［空間図形 （平面図形）］

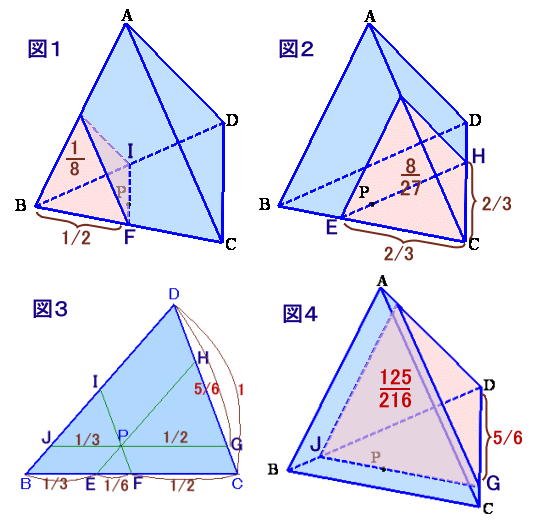
問題図 左図のような三角錐ＡＢＣＤがあり、面ＢＣＤの内部に点Ｐがあります。

点Ｐを通り、面ＡＣＤに平行な面でこの三角錐を切断すると、頂点Ｂを含むほうの立体の体積は、三角錐ＡＢＣＤの体積の８分の１倍になります。

また、点Ｐを通り、面ＡＢＤに平行な面でこの三角錐を切断すると、頂点Ｃを含むほうの立体の体積は、三角錐ＡＢＣＤの体積の２７分の８倍になります。

では、点Ｐを通り、面ＡＢＣに平行な面でこの三角錐を切断するとき、頂点Ｄを含むほうの立体の体積は、三角錐ＡＢＣＤの体積の何倍でしょうか。

解答例１

はなうさん、とまぴょんさん、遠い山のぽきょぽんさん、小学名探偵さん、ほげさん、hiroさん、ゴンともさん、受験勉強君さん、 小西孝一さん、M.Hossieさん、 他

参考図１

  • 点Ｐを通り、面ＡＣＤに平行な面（面１とします）で切断したとき（図１参照）、
    面１と辺ＢＣおよび辺ＢＤの交点をＦ、Ｉとすると、
    　点Ｂを含む三角錐の体積：三角錐ＡＢＣＤの体積＝１：８より、
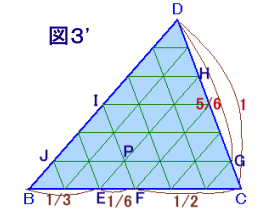
    　ＢＦ：ＢＣ＝ＢＩ：ＢＤ＝１：２。　・・・　（１）

  • 点Ｐを通り、面ＡＢＤに平行な面（面２とします）で切断したとき（図２参照）、
    面２と辺ＣＥおよび辺ＣＤの交点をＥ、Ｈとすると、
    　点Ｃを含む三角錐の体積：三角錐ＡＢＣＤの体積＝８：２７より、
    　ＣＥ：ＣＢ＝ＣＨ：ＣＤ＝２：３。　・・・　（２）

  • 点Ｐを通り、面ＡＢＣに平行な面（面３とします）で切断したとき（図４参照）、
    面３と辺ＤＣおよび辺ＤＢの交点をＧ、Ｊとすると、
    　ＤＧ：ＤＣ＝ＤＪ：ＤＢの比が分かれば、
    点Ｃを含む三角錐    の体積が求まります。

とくに面ＢＣＤだけを取り出すと（図３参照）、ＢＣの長さを１とすると、
（１）より、ＦＣ＝１−ＢＦ＝１/２、
（２）より、ＢＥ＝１−ＥＣ＝１/３。

よって、
　ＥＦ＝１−ＢＥ−ＦＣ＝１/６。

四角形ＪＢＥＰ、および四角形ＰＦＣＧはともに平行四辺形だから、
ＪＰ＝ＢＥ＝１/３、ＰＧ＝ＦＣ＝１/２、
よって、ＪＧ＝ＪＰ＋ＰＧ＝５/６。

従って、ＤＧ：ＤＣ＝ＪＧ：ＢＣ＝５/６：１、
よって、点Ｃを含む三角錐の体積：三角錐ＡＢＣＤの体積＝(５/６)3：１3＝１２５：２１６
と求まります。

答：　１２５/２１６倍

以上

（参考）図３は、下記図３’のように、△ＤＢＣの各辺を６等分して、３６個の小三角形に分割してみると分かりやすいでしょう。

参考図１-1

解答例２

はなうさん、なかさん、スモークマンさん、他

参考図２

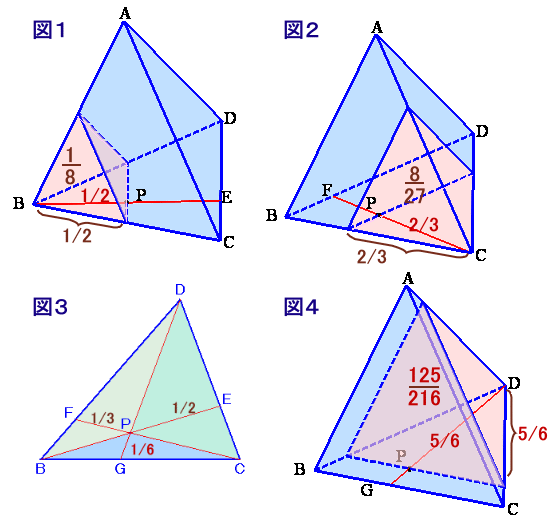
BPとＣＤの交点をＥ（図１）、ＣPとＢＤの交点をＦ（図１）、およびＤPとＢＣの交点をＧ（図４）とします。
　ＢＰ：ＢＥ＝１：２、ＣＰ：ＣＦ＝２：３。　・・・　（１）

面ＤＢＣをとくに取り出せば（図３）、（１）より、
　△ＤＰＣ：△ＡＢＣ＝ＰＥ：ＢＥ＝１：２、
　△ＤＰＢ：△ＡＢＣ＝ＰＦ：ＣＦ＝１：３。

よって、
　ＰＧ：ＤＧ＝△ＰＢＣ：△ＡＢＣ＝１−１/２−１/３＝１：６、
　ＤＰ：ＤＧ＝１−１/６＝５/６。

従って、
　点Ｃを含む三角錐の体積：三角錐ＡＢＣＤの体積＝(５/６)3：１3＝１２５：２１６
と求まります。

（その他の解法）