第３９６問の解答

問題［空間図形］

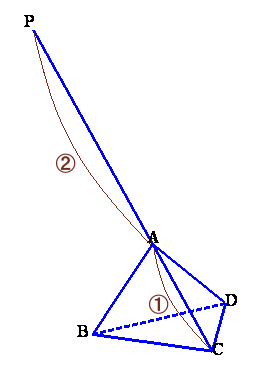問題図 左図のような三角錐ＡＢＣＤで、Pは辺ＣＡをＡ側に３倍に伸ばした点です。

同様に、

  • ＡＢをＢ側に３倍に伸ばした点をＱ
  • ＢＤをＤ側に３倍に伸ばした点をＲ
  • ＤＣをＣ側に３倍に伸ばした点をＳ

とします。

このとき、三角錐ＰＱＲＳの体積は、三角錐ＡＢＣＤの体積の何倍でしょうか。

解答例１

あ〜く＠旧Ｎさん、はなうさん、小西孝一さん、受験勉強君さん、小学名探偵さん、 他

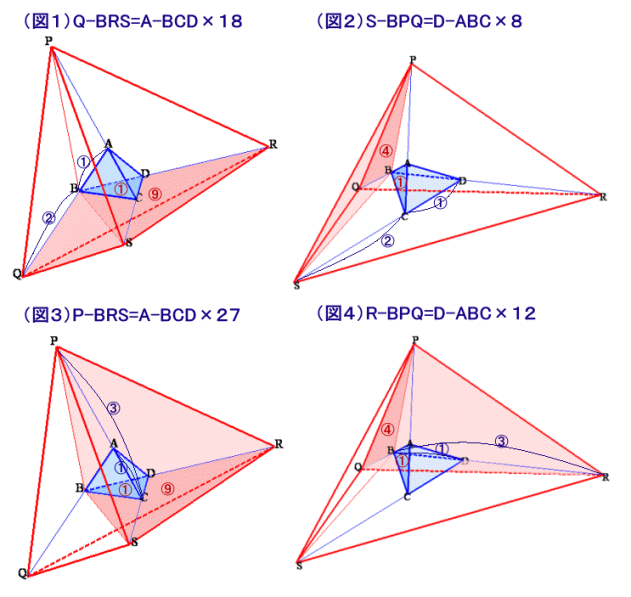
三角錐PQRSを点Bを頂点とする４つの三角錐に分割して考えます。

参考図１

（図１）三角錐Q-BRS（三角錐BQRSを頂点Qと底辺BRSで考える。以下同様）

三角錐Q-BRSと三角錐A-BCDは、底面△S-BRと△C-BDが同一平面にあります。
底辺の比＝BR：BD＝３：１、高さの比＝SD：CD＝３：１、
よって、底面△S-BR：△C-BD＝９：１となります。

また、三角錐Q-BRSと三角錐A-BCDの高さの比＝QB：BA＝２：１だから、
体積の比＝１８：１となります。

（図２）三角錐S-BPQ

三角錐S-BPQと三角錐D-ABCは、底面△P-QBと△C-ABが同一平面にあります。
底辺の比＝QB：AB＝２：１、高さの比＝PA：AC＝２：１、
よって、底面△P-QB：△C-AB＝４：１となります。

また、三角錐S-BPQと三角錐D-ABCの高さの比＝SC：CD＝２：１だから、
体積の比＝８：１となります。

（図３）三角錐P-BRS

三角錐P-BRSと三角錐A-BCDは、底面△S-BRと△C-BDが同一平面にあります。
図１と同様、底面△S-BR：△C-BD＝９：１。

また、三角錐P-BRSと三角錐A-BCDの高さの比＝PC：AC＝３：１だから、
体積の比＝２７：１となります。

（図４）三角錐R-BPQ

三角錐R-BPQと三角錐D-ABCは、底面△P-QBと△C-ABが同一平面にあります。
図３と同様、底面△P-QB：△C-AB＝４：１。

また、三角錐R-BPQと三角錐D-ABCの高さの比＝RB：DB＝３：１だから、
体積の比＝１２：１となります。

以上から、
　三角錐PQRS：三角錐ABCD＝（１８＋８＋２７＋１２）：１＝６５：１
と求まります。

答：　６５倍

以上

解答例２

なかさん、他

D、C、S、およびB、D、Rはそれぞれ一直線上に並んでいるので、R、Sは面BCDと同一平面にあります。
そこで、この平面と辺PQの交点をTとします。

参考図２

すると、C、A、P、およびA、B、Qはそれぞれ一直線上に並んでいるので、P、Qは面ABCと同一平面にあります。
従って、Tも面ABCと同一平面にあることになります。
よって、Tは辺CBの延長線上にあることが分かります。

さて、三角錐PQRSを面RSTで２分割してそれぞれの体積を求めてみましょう。

まず、三角錐P-RSTと三角錐A-BCDの高さの比＝PC：AC＝３：１、
および、三角錐Q-RSTと三角錐A-BCDの高さの比＝QB：AB＝2：１、
よって、PT：QT＝３：２となります。

△PTCと直線AQに関してメネラウスの定理より、
　CA/AP×PQ/QT×TB/BC＝１
　1/2×5/2×TB/BC＝１
よって、
　TB：BC＝４：５
となります。

△BCDの面積を１とすると、
　△DSR＝３×２＝６、
　△TCS＝９/５×２＝１８/５、
　△TBR＝４/５×３＝１２/５。

従って、△TSR
　＝△DSR＋△TCS＋△TBR＋△BCD
　＝６＋１８/５＋１２/５＋１＝１３
となります。

よって、三角錐ABCDの体積を１とすると、
　　三角錐PQRS
　＝三角錐P-RST＋三角錐Q-RST
　＝１３×（３＋２）
　＝６５
と求まります。

（参考）動く３Ｄ図

（参考）マウスでドラッグして下さい。

（その他の解法）