第399問の解答
問題[空間図形]
|
|
|
|
|
|
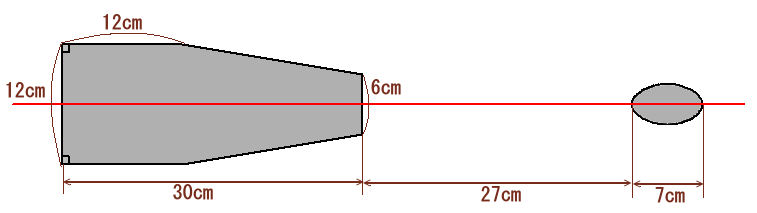
画用紙の上に立方体とボールを置いて、ある位置に豆電球を点けたところ、立方体とボールによる影が図のようになりました。(2つの影はともに赤い直線について線対称です) このとき、ボールの半径は何cmでしょうか。 |
|
|
|
|
|
解答例1
うのたかはるさん、CRYING DOLPHINさん、数楽者さん、はなうさん、なかさん、おかひで博士さん、トトロ@Nさん、あ〜く@ぴかぴかの(略さん、M.Hossieさん、小西孝一さん、始 受験勉強君さん、きょろ文さん、ほげさん、ちこりんさん、他
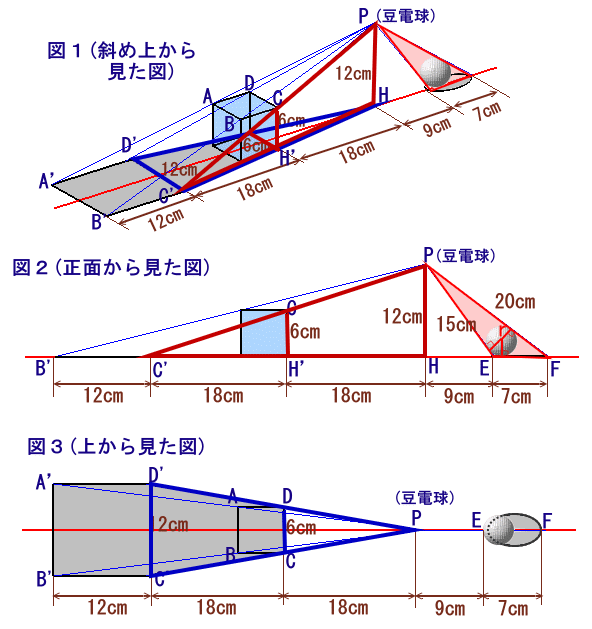
まず、豆電球がどの位置(Pとします)にあるかを考えます。
影が赤い直線に関して対称なことから、豆電球は赤い直線の真上にあることが分かります。
また、立方体の影が右から左に向かって拡がっていることから、これより右のほうにあることになります。立方体の上面の頂点をA、B、C、Dとし、これらの影となる点をA’、B’、C’、D’とします。
P、C、C’およびP、D、D’は、それぞれ一直線上に並ぶことから、
△PCDと△PC’D’は相似で、相似比は6:12=1:2、
よって、
PC:PC’=1:2
となります。線分CDとC’D’の距離は、30−12=18cmなので、PとCDとの距離も同じく18cmと分かります。
(図3参照)今度は、Pの高さを求めてみましょう。
PおよびCから赤い直線に下ろした垂線の足をHおよびH'とします。△CC'H'と△PC'Hは相似で、相似比はC'C:C'P=1:2、
よって、
PH=CH'×2=12cm
と分かります。さて、今度はボールの影を考えてみましょう。
ボールの影と赤い直線の交点を、左からEおよびFとします。直線PEおよびPFは、ボールの表面と接することになるので、
ボールを真ん中から垂直方向に切断したときの切断面、これはボールの半径rと同じ半径を持つ円になりますが、
この円は△PEFに内接することになります。さて、
△PEF=1/2×PE×PH=1/2×7×12=84cm2であり、
△PEF=1/2×PE×r+1/2×EF×r+1/2×PF×r=1/2×(PE+EF+PF)×r
となります。ところで、△PHEおよび△PHFとも辺の長さが3:4:5の直角三角形となることから、
PE=EH×5/3=15cm、PF=PH×5/3=20cmと分かります。よって、
r=△PEF×2/(PE+EF+PF)
=84×2/(15+7+20)
=2cm
と求まります。答: 2cm
以上
(参考)マウスでドラッグして下さい。
(その他の解法)
座標で解く ・・・ ゴンともさん、 他