第400問の解答
問題[ 平面図形]
|
|
|
|
|
|
|
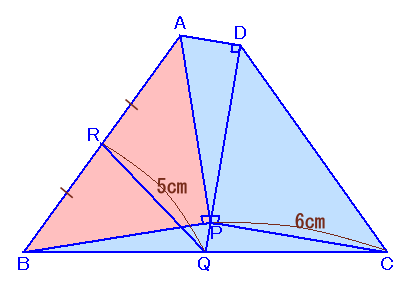 |
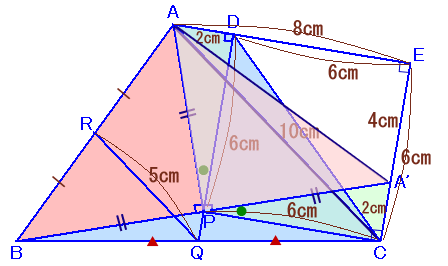
左図のような四角形ABCDがあります。 この四角形の内部に点Pをとったところ、△APB、△DPCはともに∠P=90度の直角二等辺三角形になり、DP=PC=6cmとなりました。また、∠ADP=90度となったそうです。 いま、DPの延長線と辺BCの交わった点をQ、辺ABの中点をRとすると、QR=5cmとなりました。 このとき、直角二等辺三角形APBの面積を求めてください。 |
|
|
|
|
|
|
解答例1
DCTさん、他
Cを通ってQDに引いた直線とADの延長線の交点をEとし、CEとBPの延長線の交点をA'とします。
四角形DPCEは正方形になるので、DE=EC=6cm。
△APDと△A'PCに関して、
PD=PC、∠APD=∠A'PC=90度−∠DPA'、∠ADP=∠A'CP=90度より、
1辺とその両端の角が等しいことから、△APD≡△A'PC。よって、AP=A'Pとなり、△APB≡△APA'となります。
また、△A'BCに関して、BP=PA'、およびPQとA'Cが平行となることから、
中点連結定理より、BQ=QCとなります。すると、△ABCに関して、BR=RA、BQ=QCとなることから、
中点連結定理より、AC=RQ×2=10cmと分かります。従って、△ACEはAC=10cm、CE=6cmとなり、3辺の比が3:4:5の直角三角形となります。
よって、AE=8cmと分かりますので、AD=A'C=2cm、A'E=4cmとなります。従って、△APA'=△APD+正方形DPCE−△AA'E−△A'PC
ここで、△APD=△A'PCより、
△APA'=正方形DPCE−△AA'E=6×6−1/2×8×4=20cm2よって、
△ABP=△APA'=20cm2
と求まります。答: 20cm2
以上
解答例2
あ〜く@ぴかぴかの(略さん、BossFさん、小学名探偵さん、ponta55555 さん、omegaさん、arijuneさん、他
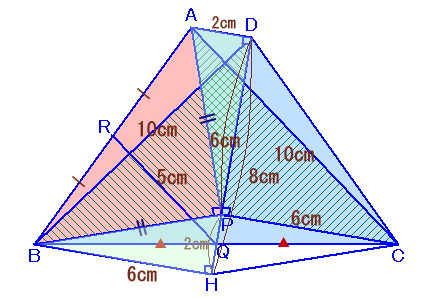
Bを通りADに平行な直線とDPの延長線の交点をHとします。
△APDと△PBHに関して、
AP=PB、∠DAP=90度−∠APD=∠HPB、∠APD=90度−∠DAP=90度−∠HPB=∠PBHより、
1辺とその両端の角が等しいことから△APD≡△PBH、
従って、BH=PD=6cmとなります。四角形PBHCに関して、
∠BHP=∠CPH=90度よりBHとPCが平行、かつBH=PC=6cmより、
△APDと△PBHは平行四辺形となります。よって、対角線BCとPHは互いに相手を2等分するので、BQ=QCとなり、
解答例1と同様、中点連結定理により、AC=RQ×2=10cmと分かります。さて、△DBPと△CAPに関して、
BP=AP、DP=CP、∠BPD=90度+∠APD=∠APCより、
2辺とその間の角が等しいことから△DBP≡△CAP、
よって、DB=CA=10cmとなります。すると、△ABHはAB=10cm、BH=6cmとなることから、3辺の比が3:4:5の直角三角形となります。
よって、AH=8cm、AD=PH=8-6=2cmと分かります。従って、
△ABP=台形ABHD−△APD−△PBH=1/2×(2+6)×8−1/2×2×6×2=20cm2
と求まります。
解答例3
CRYING DOLPHINさん、きょろ文さん、はなうさん、他
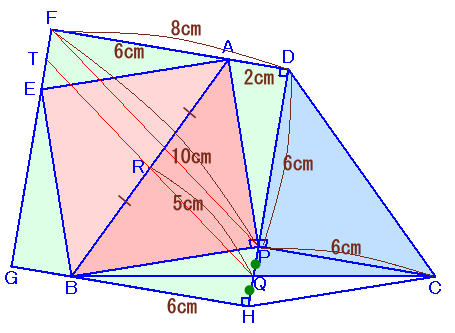
四角形FGHDおよびEBPAが正方形となるように、点Fと点Gおよび点Eをとります。
すると、点EはFG上にあり、点Rは2つの正方形の中心になります。
また、△AEF、△EBG、△BPHは△APDと合同な直角三角形となり、
AF=EG=BH=AP=6cmとなります。従って、解答例2と同様にして、
四角形PBHCが平行四辺形となり、BQ=QC、PQ=QH
と分かります。さて、FEの中点をTとすると、FT=FE×1/2=PQとなり、
四角形FTQPは平行四辺形となります、
よって、FP=TR=RQ×2=10cm。すると、△FPDは3辺の比が3:4:5の直角三角形となり、FD=8cmと分かります。
よって、AD=PH=2cm。以下、解答例2と同様。
解答例4
なかさん、経友会の進作さん、 他
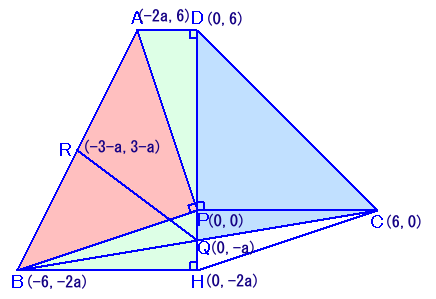
Pを原点とし、PCがx軸、PDがy軸となるような座標軸で考え、HをBからy軸に下ろした垂線の足とします。
AD=d、PH=h、BH=bとします。
題意より、
AP2=d2+62=BP2=b2+h2。 ・・・ (1)APとBPが直交することから、
−6/d×h/b=−1、
よって、h=b×d/6。 ・・・ (2)(1)に代入して、
d2+62=b2+(b×d/6)2=(b/6)2×(d2+62)
よって、b=6cm、d=hとなります。そこで、a=1/2×hとおくと、各点の座標は上図のようになります。
従って、
RQ2=(3+a)2+32=52
よって、3+a=4となり、a=1と分かります。従って、
△APB=1/2×AP2=1/2×(22+62)=20cm2
と求まります。
(その他の解法)
方程式を解 いて求める(方法はいろいろ) ・・・ Toru Fukatsuさん、始 受験勉強君さん、takaisaさん、ゴンともさん、 他
中線定理を用いる? ・・・ 藤井隆行さん、 他