第401問の解答
問題[ 平面図形]
|
|
|
|
|
|
|
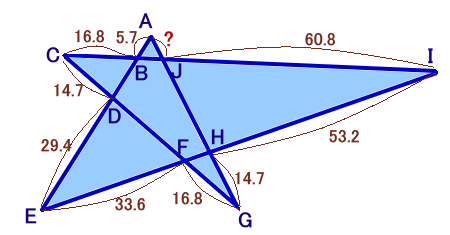 |
左図のような星形の図形ABCDEFGHIJがあります。 AB=5.7cm、BC=16.8cm、CD=14.7cm、DE=29.4cm、EF=33.6cm、FG=16.8cm、GH=14.7cm、HI=53.2cm、IJ=60.8cmであるとするとき、AJの長さ(図の?の部分の長さ)を求めてください。 (注意)今回の問題のオリジナル図形は、実際には存在しませんので、存在する図形に変更しました。 |
|
|
|
|
|
|
解答例1
CRYING DOLPHINさん、マサルさん、あ〜く@ぴかぴかの(略さん、Taroさん、DCTさん、はなうさん、takaisaさん、kasamaさん、水田Xさん、ふじさきたつみさん、tomhさん、すてっぷさん、他
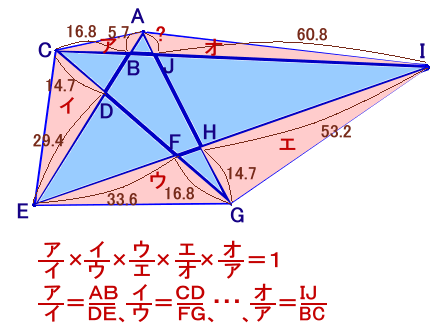
△ABC=ア、△CDE=イ、△EFG=ウ、△GHI=エ、△IJA=オ と おきます。
すると、
ア/イ×イ/ウ×ウ/エ×エ/オ×オ/ア=1
が成り立ちます。ところが、
ア/イ=AB/DE、イ/ウ=CD/FG、ウ/エ=EF/HI、エ/オ=GH/JA、オ/ア=IJ/BC
より、
5.7/29.4×14.7/16.8×33.6/53.2×14.7/JA×60.8/16.8=1従って、
JA=5.7/29.4×14.7/16.8×33.6/53.2×14.7/1×60.8/16.8=5.7cm
と求まります。答: 5.7cm
以上
解答例2
小西孝一さん、ari-juneさん、始 受験勉強君さん、他
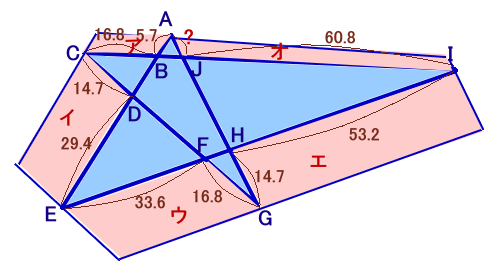
下図のような5角形をつくります。
アの面積を1とすると、
イ=ア×294/57=98/19、
ウ=イ×168/147=112/19、
エ=ウ×532/336=28/3、
オ=ア×608/168=76/21ところが、
オ:エ=AJ:14.7従って、
AJ=オ/エ×14.7=(76/21)/(28/3)×14.7=5.7cm
と求まります。
(その他の解法)
メネラウスの定理を用いて方程式を解 いて求める ・・・ ハラギャーティさん、 他