第402問の解答
問題[速さの問題]
|
|
|
|
|
|
マサルさんの乗った船Aと、トモエさんの乗った船Bが、下流のP地点を同時に出発しました。 航行の途中、マサルさんは持っていたボールを川に落としてしまい、船長さんにしつこくお願いして船を引き返してもらいました。 では、トモエさんの乗った船Bがボールとすれ違ったのは、マサルさんの乗った船Aとすれ違う何分前だったでしょうか。 |
|
|
|
|
|
解答例1
トトロ@Nさん、辻。さん、CRYING DOLPHINさん、姉小路さん、M.Hossieさん、DrKさん、あ〜く@ぴかぴかの(略さん、他
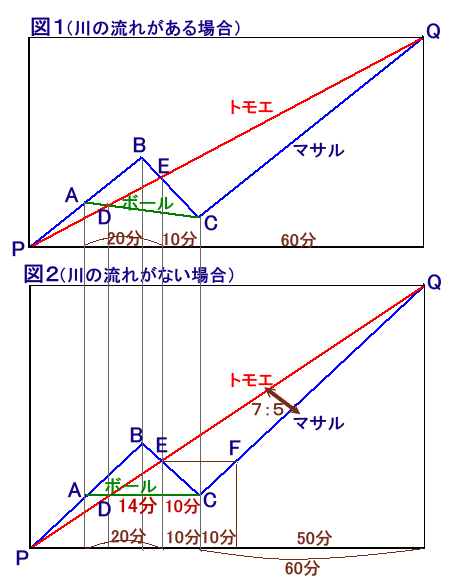
下図のようなダイアグラムで考えます。
マサルさんがボールを落とした地点をA、引き返した地点をB、ボールを拾った地点をC、
トモエさんがボールと出会った地点をD、マサルさんとすれ違った地点をE、および
マサルさんに追いつかれた地点をQとします。マサルさんの船、トモエさんの船とも同じ川の流れ分だけ常に下流に流されています。
従って、川の流れを無視して考えても良いことが分かります。図2で、マサルさんがE地点からC地点まで10分掛かったのだから、
C地点からE地点まで(今度はFとします)戻る時間も同じ10分です。すると、トモエさんがE→Qに70分掛かり、マサルさんが同じ距離(F→Q)に50分掛かったことになります。
従って、同じ距離を進むときの所要時間の比は7:5となります。さて、図2ではボールは同じ位置で浮かんでいることになるので、D→EとE→Cの距離は同じです。
従って、トモエさんがD→Eに要する時間は、マサルさんがE→Cに要する時間10分×7/5=14分と求まります。答: 14分
以上
解答例2
なかさん、小学名探偵さん、小西孝一さん、他
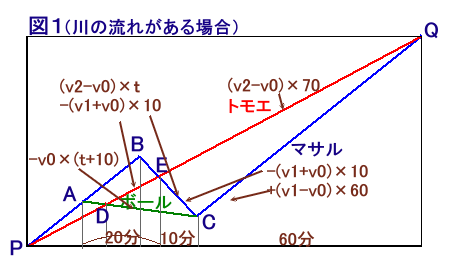
D→Eのトモエさんの所要時間をt分とします。
E→Q(トモエさん)=E→C→Q(マサルさん)より、
(v2-v0)×70=-(v1+v0)×10+(v1-v0)×60
従って、
v2×70=v1×50
よって、
v1/v2=7/5D→E(トモエさん)およびE→C(マサルさん)=D→C(ボール)より、
(v2-v0)×t-(v1+v0)×10=-v0×(t+10)
従って、
v2×t=v1×10
よって、
t=10×v1/v2=10×7/5=14分
と求まります。
(その他の解法)
方程式を解 いて求める ・・・ ゴンともさん、 他