第４０４問の解答

問題［平面図形］

問題図

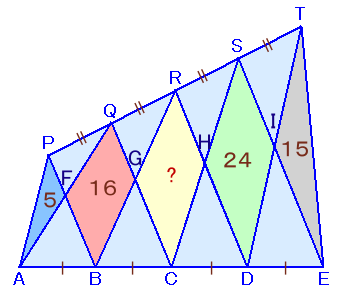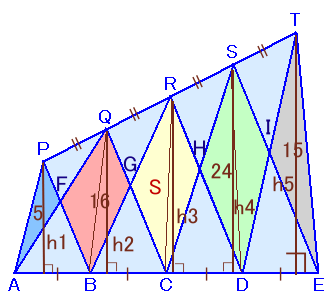
左図のような四角形ＡＥＴＰがあります。

いま、Ｂ、Ｃ、Ｄは辺ＡＥを４等分する点、Ｑ、Ｒ、Ｓは辺ＰＴを４等分する点です。このとき、△ＰＡＦ＝５cm2、四角形ＱＦＢＧ＝１６cm2、四角形ＳＨＤＩ＝２４cm2、△ＴＩＥ＝１５cm2となりました。

では、四角形ＲＧＣＨの面積は何cm2でしょうか。

解答例１

水田Xさん、小西孝一さん、他 多数
Ｐ、Ｑ、Ｒ、ＳからＡＥに下ろした垂線の高さをｈ１、ｈ２、ｈ３、ｈ４、ｈ５とし、ａ＝ＡＢとおきます。

参考図１

題意より、ＢＣ＝ＣＤ＝ＤＥ＝ａで、またｈ１、ｈ２、ｈ３、ｈ４、ｈ５は等差数列になります。

従って、
　△ＱＡＢ−△ＰＡＢ＝１/２×ａ×（ｈ２−ｈ１）
　△ＲＢＣ−△ＱＢＣ＝１/２×ａ×（ｈ３−ｈ２）
となり、ｈ２−ｈ１＝ｈ３−ｈ２より、
　△ＱＡＢ−△ＰＡＢ＝△ＲＢＣ−△ＱＢＣ
よって、
　△ＲＧＣ−△ＱＢＧ＝△ＱＦＢ−△ＰＡＦ
　△ＲＧＣ＝△ＱＢＧ＋△ＱＦＢ−△ＰＡＦ＝四角形ＱＦＢＧ−△ＰＡＦ＝１６−５＝１１ｃｍ2。

また、
　△ＳＣＤ−△ＲＣＤ＝１/２×ａ×（ｈ４−ｈ３）
　△ＴＤＥ−△ＳＤＥ＝１/２×ａ×（ｈ５−ｈ４）
となり、ｈ４−ｈ３＝ｈ５−ｈ４より、
　△ＳＣＤ−△ＲＣＤ＝△ＴＤＥ−△ＳＤＥ
よって、
　△ＳＨＤ−△ＲＣＨ＝△ＴＩＥ−△ＳＤＩ
　△ＲＣＨ＝△ＳＨＤ＋△ＳＤＩ−△ＴＩＥ＝四角形ＳＨＤＩ−△ＴＩＥ＝２４−１５＝９ｃｍ2。　

従って、
　四角形ＲＧＣＨ＝△ＲＧＣ＋△ＲＣＨ＝１１＋９＝２０ｃｍ2
と求まります。　

答：　２０cm2

以上

解答例２

ｋｕｒｉ、他

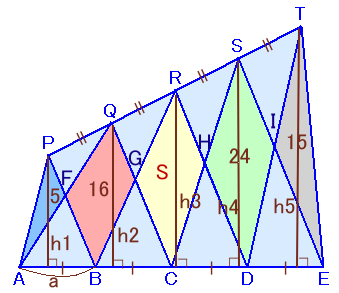
下図の記号は、解答例１と同じです。

参考図２

△ＰＡＢ＝１/２×ａ×ｈ１　・・・　（１）
△ＱＡＣ＝１/２×２ａ×ｈ２　・・・　（２）
△ＲＢＤ＝１/２×２ａ×ｈ３　・・・　（３）
△ＳＣＥ＝１/２×２ａ×ｈ４　・・・　（４）
△ＴＤＥ＝１/２×ａ×ｈ５　・・・　（５）

（１）＋（３）＋（５）より、
　△ＰＡＢ＋△ＲＢＤ＋△ＴＤＥ＝１/２×ａ×（ｈ１＋２ｈ３＋ｈ５）

ｈ１、ｈ２、ｈ３、ｈ４、ｈ５は等差数列より、ｈ１＋ｈ５＝２ｈ３より、
　△ＰＡＢ＋△ＲＢＤ＋△ＴＤＥ＝２ａ×ｈ３
従って、
　△ＰＡＦ＋四角形ＲＧＣＨ＋△ＴＩＥ＋（△ＦＡＢ＋△ＧＢＣ＋△ＨＣＤ＋△ＩＤＥ）＝２ａ×ｈ３　・・・　（６）

（２）＋（４）より、
　△ＱＡＣ＋△ＳＣＥ＝１/２×２ａ×（ｈ２＋ｈ４）

ｈ２＋ｈ４＝２ｈ３より、
　△ＱＡＣ＋△ＳＣＥ＝２ａ×ｈ３
従って、
　四角形ＱＦＢＧ＋四角形ＳＨＤＩ＋（△ＦＡＢ＋△ＧＢＣ＋△ＨＣＤ＋△ＩＤＥ）＝２ａ×ｈ３　・・・　（７）

（６）、（７）より、
　△ＰＡＦ＋四角形ＲＧＣＨ＋△ＴＩＥ＝四角形ＱＦＢＧ＋四角形ＳＨＤＩ
よって、
　四角形ＲＧＣＨ
＝四角形ＱＦＢＧ＋四角形ＳＨＤＩ−（△ＰＡＦ＋△ＴＩＥ）
＝１６＋２４−（５＋１５）
＝２０ｃｍ2
と求まります。　

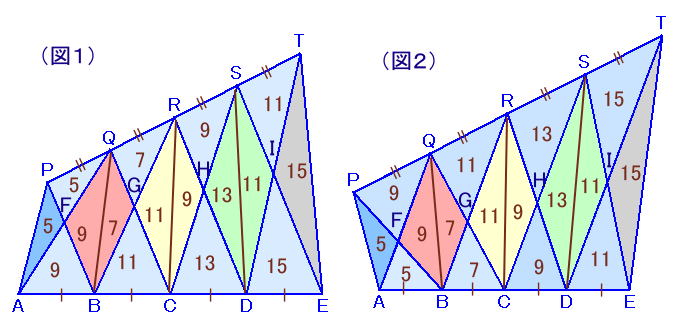
（参考）本問では、下図のように２通りのタイプの図形が存在します。

参考図３