第406問の解答
問題[ 平面図形]
|
|
|
|
|
|
|
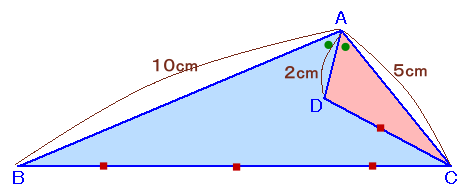 |
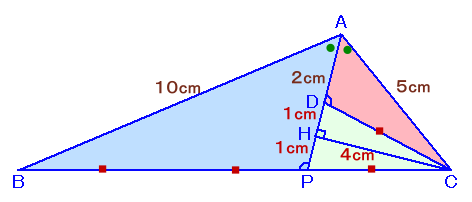
左図のような、AB=10cm、AC=5cmである△ABCがあります。 いま、∠Aの二等分線上にAD=2cmとなる点Dをとり、CとDを結んだところ、CD:BC=1:3となりました。(ただし、点Dは、△ABCの内部(辺上は含みません)にあるものとします。) このとき、ADCの面積を求めてください。 |
|
|
|
|
|
|
解答例1
takaisaさん、姉小路さん、、辻。さん、uchinyanさん、なかさん、他
ADの延長とBCの交点をPとし、CからAPに下ろした垂線の足をHとします。
APは∠BACの二等分線だから、
BP:PC=AB:AC=2:1。よって、PC=DC=BP×1/3となり、△CDPは二等辺三角形となります。
従って、∠CDP=∠CPD、
よって、∠ADP=180°-∠CDP=180°-∠CPD=∠APB。すると、△ABPと△ACPは2つの角が等しいので相似、
従って、AP:AB=AD:AC、
よって、AP=AB×AD/AC=10×2/5=4cm。従って、DP=AP-AD=4-2=2cm。
よって、HはDPの中点だから、DH=HP=1cm。よって、AH=AD+DH=2+1=1cm。
すると、△CAHは辺の長さが3:4:5の直角三角形となり、
CH=4cmと求まります。よって、
△ADC=1/2×AD×CH=1/2×2×2=4cm2
と求まります。答: 4cm2
以上
解答例2
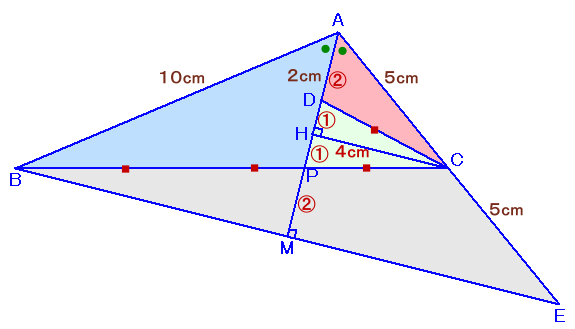
始 受験勉強君さん、すてっぷさん、他
ACを延長してCE=ACとなるように点Eをとります。
また、ADを延長し、BC、BEとの交点をP、M、およびCからAMに下ろした垂線の足をHとします。
AB=AE=10cmより、△ABEは二等辺三角形となり、
∠BAM=∠CAMよりAMはBEの垂直二等分線となります。よって、HCとMEは平行となり中点連結定理より、
HC=ME×1/2。△PBMと△PCHは、∠BPM=∠CPH(対頂角)、∠PMB=∠PHC=90°より相似、
従って、BP:PC=BM:CH=ME:HC=2:1、PM:PH=2:1。よって、PC=BC×1/3=DCとなり、△CDPは二等辺三角形と分かります。
ここで、DH=HP=①とすると、PM=②、AH=HM=③より、AD=AH-AD=②、
よって、DH=HP=1cmと求まります。
以下同様。
解答例3
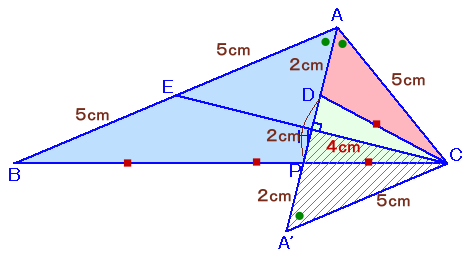
小西孝一さん、他
点EをABの中点とし、Cを通りABに平行な直線とADの延長線の交点をA'とします。
また、AA'とCEおよびBCとの交点をH、Pとします。
△AECは二等辺三角形で、∠EAH=∠CAHより、AHはECの垂直二等分線となります。
また、ABとA'Cは平行だから∠CA'A=∠BAA'=CAA'、
よって、△CAA'はCA=CA'=5cmの二等辺三角形と分かります。さらに、△ABPと△A'CPは、∠APB=∠A'PC、∠BAP=∠CA'Pより相似、
BP:PC=AB:A'C=2:1、
よって、PC=BC×1/3=DCとなり、△CDPは二等辺三角形と分かります。また、△CA'Pと△CADは、∠CPA'=CAD、∠CA'P=CADより、相似かつCA'=CAより合同、
よって、A'P=AD=2cmとなります。さらに、AP=A'P×2=4cmより、DP=AP-AD=2cm、
よって、DH=HP=1cmと求まります。
以下同様。
解答例4
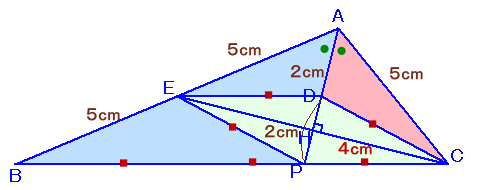
きょろ文さん、他
点EをABの中点、点PをADとBCの交点、点HをECとAPの交点とします。
APは∠BACの二等分線だから、BP:PC=AB:AC=2:1、
よって、PC=BC×1/3=DC。また、△AECは、AE=AC=5cmの二等辺三角形だから、
AHはECの垂直二等分線となり、DE=DC、PE=PC。
よって、四角形EPCDは菱形と分かります。すると、EDはBCと平行で、EはABの中点だから、中点連結定理より、
DはAPの中点、
従って、DP=AD=2cm。よって、DH=HP=1cmと求まります。
以下同様。
(その他の解法)
余弦定理を用いてcosθを求める ・・・ ゴンともさん、M.Hossieさん、 他
θ=∠BAD=∠CADとおくと、50*(cosθ)^2-45*cosθ+9=0よりcosθ=3/5
(cosθ=-3/10はDがBC上になりより不適)
sinθ=4/5 、△ADC=(AD*AC*sinθ)/2=(2*5*4/5)/2=4cm2
CADで書き面積を求めた ・・・ kasamaさん、 他