第407問の解答
問題[整数の性質]
|
|
|
|
|
|
ある10ケタの整数があります。この整数は、以下のような性質を持っています。
また、この整数は、各位に使われる数字が全て異なっています。 |
|
|
|
|
|
解答例1
辻。さん、呑さん、、あ~く@ぴかぴかの(略さん、始 受験勉強君さん、おかひで博士さん、姉小路さん、圭太さん、小西孝一さん、Toru Fukatsuさん、M.Hossieさん、水田Xさん、DrKさん、なかさん、ゴンともさん、uchinyanさん、すてっぷさん、ちこりんさん、n厨さん、他
求める整数をX=ABCDEFGHIJとし、「上nケタの数は、nで割りきれる」という条件を「条件n」と いうことにします。
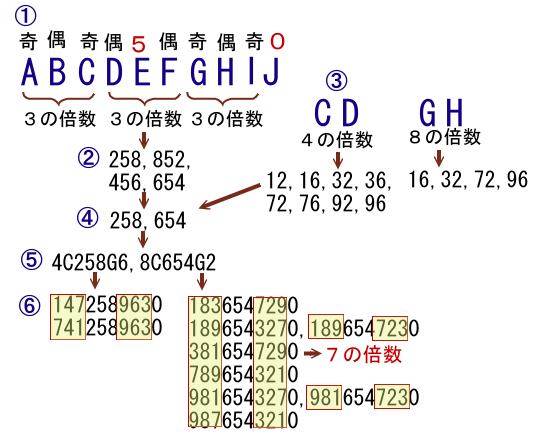
(ステップ①)
条件10よりJ=0、条件5よりE=5と決まります。
条件2、条件4、条件6、条件8より、B、D、F、Hは偶数(2、4、6、8)となるので、
A、C、G、Iは奇数(1、3、7、9)と分かります。(ステップ②)
条件3、条件6、条件9よりABC、ABCDEF、ABCDEFGHIは3の倍数(各位の数字の和が3)となります。
条件6の(A+B+C)+(D+E+F)が3の倍数は、条件3よりA+B+Cが3の倍数だから、(D+E+F)が3の倍数、あとはFが偶数なのでABCDEFが6の倍数という条件はOK。
条件9も同様にしてG+H+Iが3の倍数となりますが、最終的にはA+B+C+・・・+I=1+2+・・・+9=45だからOK。
さて、DEFはE=5と決まっているので、D+5+Fが3の倍数となるのは、
(D、F)=(2、8)、(8、2)、(4、6)、(6、4)の組み合わせのみとなります。(ステップ③)
条件4よりABCDは4の倍数となりますが、ABCD=AB×100+CDで100=25×4だから、CDが4の倍数となります。
ところが、Cは奇数(1、3、7、9)なので、このような4の倍数は、CD=12、16、32、36、72、76、92、96、従ってD=2、6のいずれかとなります。
また、条件8よりABCDRFGHは8の倍数となりますが、ABCDEFGH=ABCDEF×100+GHで100=25×4でしかもFは偶数だから、ABCDEF×100は8の倍数、従ってGHが8の倍数となります。
ところが、Gは奇数(1、3、7、9)なので、このような8の倍数は、GH=16、32、72、96、従ってH=2、6のいずれかとなります。(ステップ④)
ステップ③より(D、H)=(2、6)、(6、2)となるので、F=2または6とはなりません。
従って、ステップ②で求まったDEF=852、456は不適、DEF=258、654のどちらかになります。(ステップ⑤)
DEF=258のとき、H=6、従ってB=4となり、BCDEFGH=4C258G6
DEF=654のとき、H=2、従ってB=8となり、BCDEFGH=8C654G2
のいずれかとなります。(ステップ⑤)
BCDEFGH=4C258G6のとき、A+4+Cが3の倍数となるのは、(A、B)=(1、7)、(7、1)の2通り。このとき(G、I)=(3、9)、(9、3)ですが、ステップ③の結果よりGH=96のみが適します。
従って、X=1472589630、7412589630の2通り。
BCDEFGH=8C654G2のとき、A+4+Cが3の倍数となるのは、(A、B)=(1、3)、(1、9)、(3、1)、(3、7)、(7、3)、(7、9)、(9、1)、(9、7)、の8通り。
それぞれについてステップ③のGHに適するものに絞っていけば、X=1836547290、1896543270、1896547230、3816547290、7896543210、9816543270,9816547230,9876543210の8通りとなります。(ステップ⑥)
ステップ⑤で絞られた合計10通りの整数のなかで、条件7を満たすものはX=3816547290のみ。これが求める整数となります。
答: 3816547290
以上
(その他の解法)
プログラムで調べる ・・・ ミキティさん、まるケンさん、ちこりんさん、kasamaさん、ハラギャーテイさん、???さん、ちこりんさん、 他