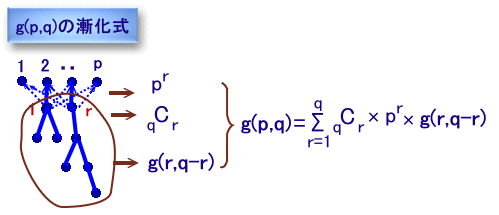第408問の解答
問題[場合の数]
|
|
|
|
|
|
ある湖の上に、5つの島があります。
(注)常識的でない橋のかけ方(1つの島を飛び越して別の島に橋をかける、等)をしても構わないものとします。 |
|
|
|
|
|
解答例1
あ〜く@ぴかぴかの(略さん、CRYING DOLPHINさん、Taroさん、まるケンさん、tomhさん、BossFさん、小西孝一さん、他
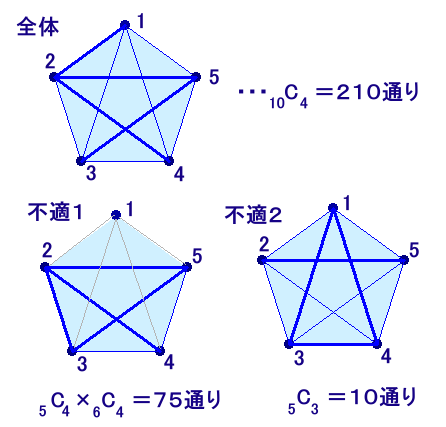
島を頂点、橋を辺で表すことにします。全ての頂点どうしを辺で結んだ場合から不適なものを除いて数えることにしましょう。
辺の数は全部で5つの頂点から2個選ぶ、5C2=10通りあります。
従って、10個の辺から4本選ぶのは、全部で10C4=210通りあります。さて、これらから題意に不適なものは2つのタイプがあります。
(タイプ1)4頂点しか結んでいない場合
最初に5個の頂点から4個選ぶのが、5C4=5通りあります。
選んだ4個の頂点の辺の数は全部で4C2=6通り、これらから4本選ぶのは6C4=15通り、
従って、タイプ1は全部で5C4×6C4=5×15=75通りとなります。(タイプ2)三角形と1本の辺になる場合
5個の頂点から3個選ぶ5C3=10通りあります。
よって、求める場合の数は、
210−(75+10)=125通り
となります。答: 125通り
以上
解答例2
まるケンさん、圭太さん、なかさん、tomhさん、DrKさん、トトロ@Nさん、ちこりんさん、おかひで博士さん、kasamaさん、他
1つの頂点から結ばれた辺の個数の最大値が何本かで場合分けしてみます。
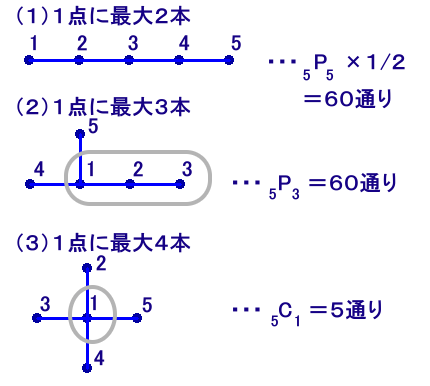
(タイプ1)最大が2本のとき
5つの頂点が1列に並んだ形状となります。
従って、5つの頂点を5個並べる順列の数=5P5=5!=5×4×3×2×1=120通り、
ただし左右ひっくり返したものは同じものになるので、この半分の60通りになります。(タイプ2)最大が3本のとき
3本の辺が集まる1つの頂点と、これから2つ続く頂点が決まれば、あとの2頂点は自動的に決まるので、5P3=5×4×3=60通りとなります。
(タイプ3)最大が4本のとき
4本の辺が集まる1つの頂点が決まれば、あとの4頂点は自動的に決まるので、
5C1=5通りとなります。従って、求める個数は、
60+60+5=125通り
になります。
解答例3
姉小路さん、他
頂点の数がn個のときをtnで表して、漸化式を求めて数えることににします。
ただし、形状に注目すると一般化できないので、1つの頂点を固定したツリー状で数えることにします。
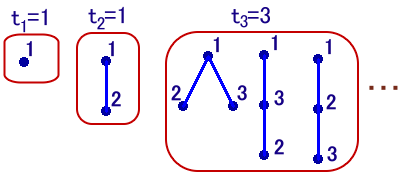
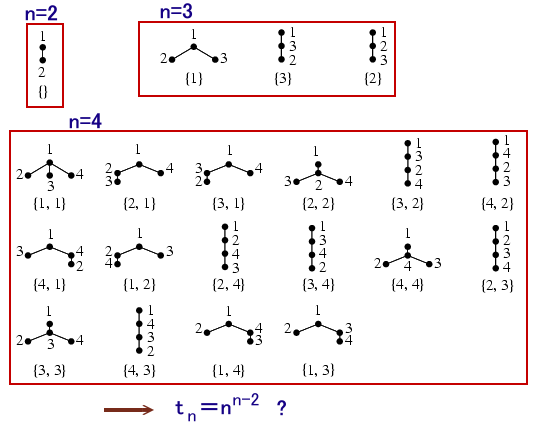
n≦3までの個数は、上記のようにt1=1、t2=1、t3=3と簡単に求まります。
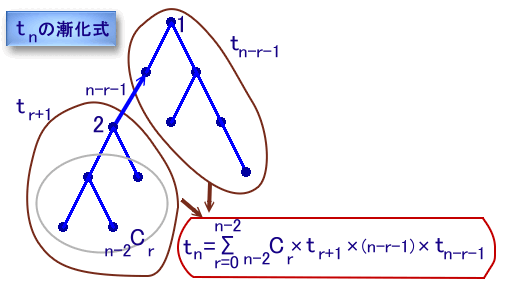
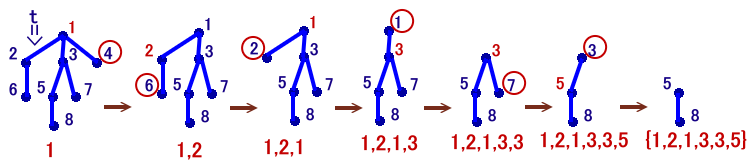
n≧3のときの漸化式を下図で考えてみましょう。
各頂点には1からnまでの番号を振っておき、頂点1を固定しておきます。
さて頂点2にぶら下がっている頂点の個数をr個とすると、0≦r≦(n-2)となります。まず頂点1と頂点2を除く(n-2)個の頂点からr個選ぶのが、n-2Cr通り。
頂点2からr個の頂点がぶら下がるツリーは、tr+1通り、
また頂点1から残り(n-r-2)個の頂点がぶら下がるツリーはtn-r-1通り。そして、頂点2が頂点1からのツリーのどの頂点にぶら下がるかは、(n-r-1)通り、
従って、漸化式は下記のようになります。tn=Σ(r=0..n-2){n-2Cr×tr+1×(n-r-1)×tn-r-1} ・・・ (1)
すると、
t3=1C0×t1×2×t2+1C1×t2×1×t1
=1×1×2×1+1×1×1×1
=2+1=3t4=2C0×t1×3×t3+2C1×t2×2×t2+2C2×t3×1×t1
=1×1×3×3+2×1×2×1+1×3×1×1
=9+4+3=16t5=3C0×t1×4×t4+3C1×t2×3×t3+3C2×t3×2×t2+3C3×t4×1×t1
=1×1×4×16+3×1×3×3+3×3×2×1+1×16×1×1
=64+27+18+16=125と順次求まります。
解答例4
まるケンさん、uchinyanさん、 他
tn=nn-2と予想されますが、(1)の漸化式ではこのことを証明するのが難しいので、
複数のツリーが集まったものに拡張して考えることにしましょう。
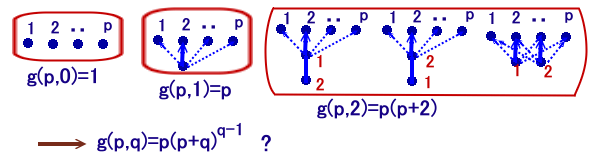
p本のツリーが集まった場合で、これらにぶら下がった頂点の個数が全部でq個のときの場合の数を、
g(p、q)で表すことにします。
容易に、g(p、0)=1、g(p、1)=p、g(p、2)=p(p+2)と求まります。
どうも
g(p、q)=p(p+q)q-1 ・・・ (2)
が成り立ちそうです。これをqに関する漸化式を求めて証明することにしましょう。
p本のツリーで固定された各頂点(根と呼びます)に直接ぶら下がる頂点の個数をrとします。
1≦r≦qで、これらを選ぶのがqCr通り。このr個の頂点を根として考えると、r本のツリーに(q-r)個の頂点がぶら下がっているので、
全部でg(r、q−r)通りあります。そして、r個の根が元のp個の根のどれにぶら下がるかは、それぞれp通りあるので、
全部でpr通り。従って漸化式は、下記のようになります。
g(p、q)=Σ(r=1..q){qCr×pr×g(r、q-r)} ・・・ (3)
あるqの値未満について(2)が成り立つと仮定しましょう。
すると(3)より、
g(p、q)=Σ(r=1..q){qCr×pr×r×qq-r-1}
=Σ(r=1..q){(q-1Cr-1×q/r)×pr×r×qq-r-1}
=Σ(r=0..q-1){q-1Cr×pr+1×qq-r}
=p(p+q)q-1
となり、qについても(2)が成り立ちます。従って、数学的帰納法より(2)が成り立つことが分かります。
とくにツリーが1本のとき、(2)より、
tn=g(1、n-1)=1×(1+n-1)n-1-1=nn-2
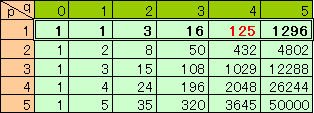
が得られます。(参考)1≦p、q≦5のときのg(p、q)
解答例5
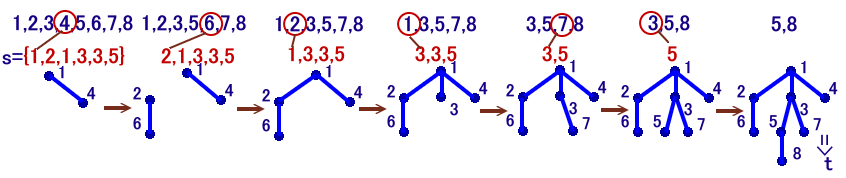
Prüfer符号(下図参照)との対応によって(2)を直接証明してみます 。
頂点がn個のときのツリー全体をT、1〜nまでの数をn-2個並べてできる集合をSとし、t∈Tについて、s(
Prüfer符号 )を次のように定めます。
(1):端点(つながっている辺が1本しかない頂点)のうち最小番号のものをa1とし、a1につながっている頂点をb1とします。
(2):tからa1を除いたツリーについて、同様にして最小番号の端点a2と、a2につながる頂点b2を求めます。
以下、(n-2)回の操作を行って得たbk(k=0..n-2)を並べて、s={b1b2・・・bn-2}とします。
このとき、1≦bk≦nより、s∈Sとなります。逆に、s∈Sに対し、tを次のように定めます。
まず、N={1、2、・・・、n}、s={b1b2・・・bn-2}(1≦bk≦n)とします。
(1):Nに属する整数でsに含まれないものの最小値をa1とし、a1とb1を結びます。
(2):Nからa1を、sからb1をそれぞれ除き、同様に求めたa2とb2を結びます。
以下、(n-2)回の操作を行うと、sはなくなり、Nには2個の整数が残ります。
残ったNの2整数に対する2頂点を結んで操作を終えます。できあがった図形をtとすると、tにはn個の頂点と(n-1)本の辺が含まれます。
もしtがp本の(つながっていない)ツリーに分かれていたとすると、m個の頂点からなるツリーには(m-1)本の辺からできているので、tの辺は(n-p)本となり矛盾します。
従って、tは1本のツリーとなり、t∈Tになります。以上から、Tの個数=Sの個数=nn-2となることが分かります。