第４０９問の解答

問題［割合（確率）］

マサルさん、ツヨシ君、トモエさんの３人がジャンケンで１位、２位、３位を決めようとしています。
このとき、１０回目のジャンケンでようやく３人の順位が決まる確率（確からしさ）を求めてください。
ただし、あいこも１回と数えるものとします。

（注１）３人とも、３分の１の確率でグー、チョキ、パーのうち１つを選んで出すものとします。
（注２）順位は、勝ち抜け（あるいは負け抜け）方式で決定します。例えば、最初３人でジャンケンを行い、
　　　１人が勝ち抜け（または負け抜け）したら、残りの２人で２位決定戦（または決勝戦）を行って１位〜３位を決定します。

解答例１

Taroさん、辻。さん、uchinyanさん、tomhさん、takaisaさん、つよしさん、なかさん、小西孝一さん、始 受験勉強君さん、圭太さん、kasamaさん、mhayashiさん、ねすけさん、N.Nishiさん、患者猫ぼのさん、うのたかはるさん、うーさん、ゴンともさん、姉小路さん、RYO-chinさん、他 多数

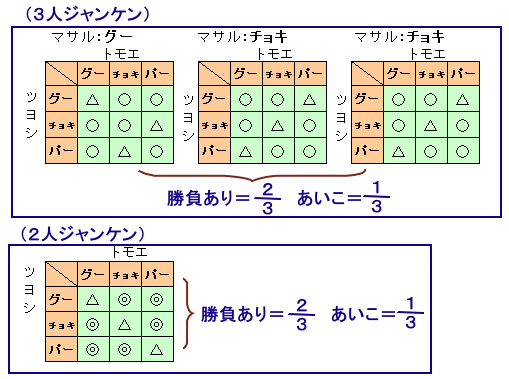
参考図１−０

３人がジャンケンしたとき：
勝負あり（１人が勝ち抜けまたは負け抜けする）の確率＝１８/２７＝２/３
あいこの確率＝９/２７＝１/３

２人ジャンケンのとき：
勝負ありの確率＝６/９＝２/３
あいこの確率＝３/９＝１/３

となります。

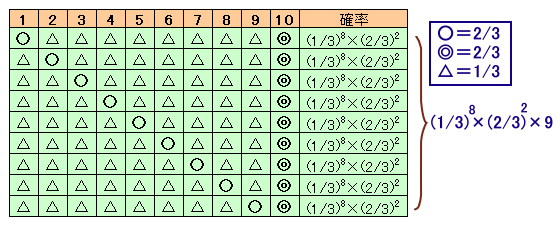
１０回目のジャンケンでようやく３人の順位が決まる には、
１回目から９回目のいずれか１回で３人ジャンケンの勝負がつき（３人→２人）、
１０回目で２人ジャンケンの勝負がつくことになります（残りの８回はすべてあいこ）。

参考図１

従って、
　求める確率＝（１/３）8×（２/３）2×９＝４/６５６１
と求まります。

答：　 ４/６５６１

以上

解答例２

CRYING DOLPHINさん、M.Hossieさん、他

漸化式を求めて計算してみます。

参考図２

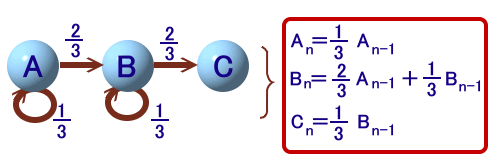
n回目のジャンケンが終わって、まったく順位がつ いていない確率をＡn、２人の順位が決まっていない確率をＢn、３人の順位がちょうど決まる確率をＣnとします。（便宜上、最初の状態をＡ0＝１、B0＝０、C0＝０とします。）

すると、
　Ａn＝１/３×Ａn-1　・・・　（１）
　Bn＝２/３×Ａn-1＋１/３×Bn-1　・・・　（２）
　Cn＝２/３×Bn-1　・・・　（３）
となります。

（１）より、Ａnは、初項がＡ0＝１、公比が１/３の等比数列となるので、
　Ａn＝（１/３）nと分かります。

従って（２）より、
　Bn−１/３×Bn-1＝２/３×（１/３）nと
　Bn×３n−Bn-1×３n-1＝２/３　・・・　（４）
となります。

（４）より、Bn×３nは、初項がB0×３0＝１、公差が２/３の等比数列となるので、
　Bn×３n＝２/３×ｎ
　Bn＝２/３×ｎ×（１/３）n-1　・・・　（５）
と分かります。

よって（５）より、
 Cn＝２/３×２/３×（ｎ−１）×（１/３）n-2　
　　＝４×（ｎ−１）×（１/３）n　・・・　（６）
となります。

よって、１０回目に順位が決まる確率は、
　C10＝４×９×（１/３）10＝４/６５６１
と求まります。