第410問の解答
問題[平面図形]
|
|
|
|
|
|
|
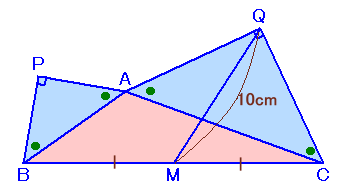 |
左図のように、△ABCの辺ACを一辺とし、QA=QCである直角二等辺三角形QACと、辺ABを一辺とし、PA=PBである直角二等辺三角形PABを△ABCの外側に作りました。 また、辺BCの中点をMとし、QとMを結んだところ、QM=10cmとなりました。 このとき、五角形APBCQ(△ABC+△PAB+△QAC)の面積を求めてください。 |
|
|
|
|
|
|
解答例1
あ〜く@ぴかぴかの(略さん、hiroさん、消しゴムパトロールさん、小西孝一さん、きょろ文さん、uchinyanさん、他
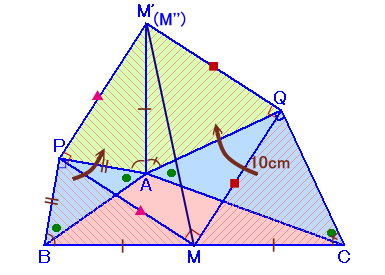
Pを中心に△PBMを反時計回りに90度回転(頂点BがAに移動)したものを△PAM’、
Qを中心に△QCMを90度回転(頂点CがAに移動)したものを△QAM’’とします。
(∠M’AP+∠M’’AQ)+(∠PAB+∠BAC+∠QAC)
=(∠PBM+∠QCM)+(∠PAB+∠BAC+∠QAC)
={(45°+∠ABC)+(45°+∠ACB)}+(45°+∠BAC+45°)
=45°×4+(∠ABC+∠ACB+∠BAC)
=180°+180°=360°従って、辺M’Aと辺M’’Aは重なることが分かります。
ところが、M’A=MB=MC=M’’Aより、頂点M’とM’’は一致する ことになります。さて、
∠M’PM=∠M’PA+∠APM=∠MPB+∠APM=90°、
∠M’’QM=∠M’’QA+∠AQM=∠MQC+∠APM=90°よって、△M’PMと△M’’QMは、それぞれ直角二等辺三角形になり、
かつ斜辺M’Mが共通なので、これらは合同となります。従って、四角形M’PMQは1辺が10cmの正方形となります。
よって、
五角形APBCQ
=四角形APMQ+△PBM+△QCM
=四角形APMQ+△PAM’+△QAM’
=正方形M’PMQ
=10×10=100cm2
と求まります。答: 100cm2
以上
解答例2
arijuneさん、他
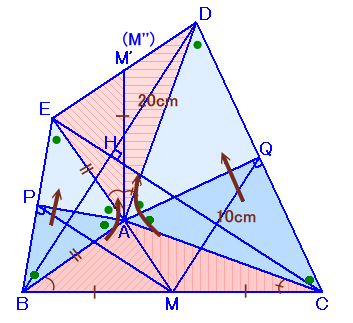
AQに関するCの対称点をD、APに関するBの対称点をEとします。
さらに、△ABMをAがE、BがAと一致するように移動したものを△EAM’、
および、△ACMをAがD、CがAと一致するように移動したものを△DAM’’とします。
(∠EAM’+∠DAM’’)+(∠EAB+∠BAC+∠DAC)
=(∠ABM+∠ACM)+(90°+∠BAC+90°)
=(∠ABM+∠ACM+∠BAC)+90°×2
=180°+180°=360°従って、辺M’Aと辺M’’Aは重なることが分かります。
また、M’A=BM=CM=M’’Aとなることから、M’とM’’は一致することになります。さて、BM=CM、DQ=CQだから、中点連結定理により、
BDとMQは平行で、BD=MQ×2=20cmとなります。また、△BADと△EACについて、
BA=EA、AD=AC、∠BAD=90°+∠EAD=∠EACより、
2辺と挟角が等しいので合同となります。2つの三角形はBAがEAになることから90°回転したことになるので、
BD=EC=20cmで、BDとECは直交することが分かります。よって、
四角形EBCD=1/2×EC×BD=1/2×20×20=200cm2従って、
五角形APBCQ=1/2×四角形EBCD=100cm2
と求まります。
解答例3
omegaさん、他
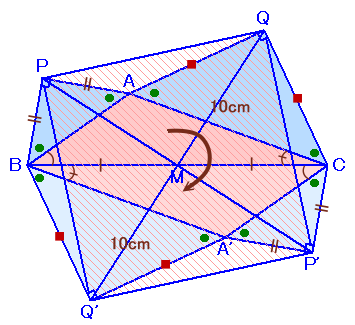
五角形APBCQを180°回転したものをA’P’CBQ’とします。
すると、PQとQ’P’は、平行かつ長さが等しいので、四角形PQ’P’Qは平行四辺形となります。
また、PMP’とQMQ’は、それぞれ一直線となるので、平行四辺形PQ’P’Qの対角線になります。さて、△PAQと△P’CQについて、
PA=PB=P’C、QA=QC、∠PAQ=270°−∠BAC=90°+∠ABC+∠ACB=∠P’CQ
となり、2辺と挟角が等しいので合同となります。同様に、△PBQと△P’A’Q’も合同となり、これら4つの三角形はすべて合同となります。
従って、平行四辺形PQ’P’Qは菱形になります。
さて、∠PQP’=∠PQA+∠AQP’=∠P’QC+∠AQP’=90°、
よって、菱形PQ’P’Qは、1辺が10cmの正方形と分かります。以上から、
五角形APBCQ+五角形A’P’CBQ’=正方形PQ’P’Q=10×10×2=200cm2
よって、
五角形APBCQ=1/2×200cm2=100cm2
と求まります。
解答例4
水田Xさん、他
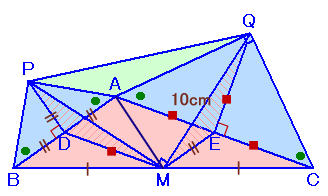
ABの中点をD、ACの中点をEとします。
△PABは直角二等辺三角形だから、PD=BD=ADで、PDとABは直交します。
同様に、△QACは直角二等辺三角形だから、QE=AE=ACで、QEとACは直交します。また中点連結定理より、
DMはACと平行で、DM=1/2×AC=QE、および
EMはABと平行で、EM=1/2×AB=PD
となります。よって、四角形ADMEは平行四辺形となります。
また、
∠PDM=90°+∠ADM=90°+∠AEM=∠QEMよって、△PDMと△MEQは、2辺と挟角が等しいので合同と分かります。
さて、
∠PMQ
=180°−(∠DMB+∠PMD+∠QME+∠EMC)
=180°−(∠DMB+∠PMD+∠MPD+∠DBM)
=∠DPB+∠DBP=90°よって、△PMQは直角二等辺三角形と分かります。
また、PA:PD=QA:QE=√2:1で、
∠PAQ=270°−∠BAC
=90°+∠ABC+∠ACB
=90°+∠DBM+∠DMB
=90°+∠ADM
=∠PDMよって、△PAQは、△PDMおよび△MEQと相似で、相似比は√2:1
従って、△PAQ=△PDM+△MEQとなります。
よって、
△PDA+△ADM+△QAE+△AEM
=△PAQ+△ADM+△QAE
=△PMQところが、
△PDB=△PDA、△BDM=△ADM、△QCE=△QAE、△CEM=△AEM
より、
△PDB+△BDM+△QCE+△CEM
=△PDA+△ADM+△QAE+△AEM
=△PMQよって、
五角形APBCQ=2×△PMQ=2×(1/2×10×10)=100cm2
と求まります。
(その他の解法)
10√2*5√2=100 ・・・ takaisaさん、 他
△ABCが直角二等辺三角形など特殊な場合を想定して解く ・・・ トトロ@Nさん、AЯOTさん、うのたかはるさん、まるケンさん、mhayashiさん、長野 美光さん、始 受験勉強君さん、辻。さん、fファルコンさん、姉小路さん、tomhさん、うーさん、ハラギャーテイさん、M.Hossieさん、dottoreさん、さいと散さん、 他 多数
問題の図形をCadで作図 して計算 ・・・ kasamaさん、他
ベクトルで解く ・・・ Toru Fukatsuさん、他
複素数を使って解く ・・・ uchinyanさん、他