第411問の解答
問題[整数の性質 ]
|
|
|
|
|
|
1〜6の数字の書かれたカードがたくさんあります。
これらのカードを使って、2でも3でも5でも割りきれない整数を小さいほうから順に作ることにします。 このときできる整数のうち、小さいほうから345番目の整数を求めてください。 |
|
|
|
|
|
解答例1
あ〜く@ぴかぴかの(略さん、DrKさん、辻。さん、数楽者さん、なかさん、始 受験勉強君さん、つよしさん、AMさん、小西孝一さん、ゴンともさん、M.Hossieさん、でんきやさん、きょろ文さん、姉小路さん、他
4桁までの整数をN=ABCDとして考えてみます。
D=1、3のとき ・・・ Nは、2の倍数でも5の倍数でもない
D=2、4、6のとき ・・・ Nは、2の倍数
D=5のとき ・・・ Nは、5の倍数
従って、D=1、3が3の倍数でないものを数えれば良いことになります。
Nが、1桁のとき ・・・ D=1は適し、D=3は3の倍数だから不適
→ 1個
Nが、2桁以上のとき ・・・ A、Bを固定して考えます。
3の倍数かどうかは、各桁の数字合計が3の倍数かどうかで判断できます。
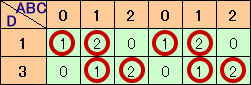
さて、、C=1から6の連続した整数となりますので、
ABCを3で割った余りは、0、1、2が均等に、それぞれ2個ずつになります。ABCを3で割った余りと、D=1、3との組み合わせで、Nを3で割った余りは、下表のようになります。
従って、8個ずつあることが分かります。
2桁の整数は、A=0、B=0 ・・・ 1通り×8=8個
3桁の整数は、A=0、B=1から6 ・・・ 6通り×8=48個
4桁の整数は、A=1から6、B=1から6 ・・・ 6×6通り×8=288個従って、4桁までの整数では、
1+8+48+288=345個
となります。よって、 求める整数は、4桁の整数で最も大きい整数となります。
6663は、3の倍数なので、6661が345番目の整数と分かります。
答: 6661
以上
解答例2
uchinyanさん、他
1桁の整数では1の1個、2桁から4桁の整数N=ABCDで数えましょう。
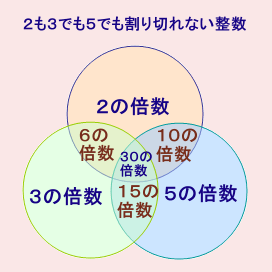
2でも3でも5でも割りきれない整数(の個数)
=全体−(2の倍数+3の倍数+5の倍数)+(6の倍数+10の倍数+15の倍数)−30の倍数
と数えることができます。AとBを固定して、C=1から6、D=1から6の、6×6=36個で考えましょう。
2の倍数 ・・・ D=2、4、6、Cは任意、3×6=18個
3の倍数 ・・・ Cを固定すると、D=1から6までの連続整数だから2個×6=12個
5の倍数 ・・・ D=5、Cは任意、1×6=6個
6の倍数 ・・・ Cを固定すると、D=1から6までの連続整数だから1個×6=6個
10の倍数 ・・・ D>0なので、10の倍数はない
15の倍数 ・・・ 15の倍数は、D=5で、かつ3の倍数。
C=1から6まで変わるとき、3で割った余りは均等にでてくるので、3の倍数は2個30の倍数 ・・・ D>0なので、30の倍数はない
従って、
36−(18+12+6)+(6+0+2)−0=8個
ずつあることが分かります。以下、同様。
(その他の解法)
プログラムで数える ・・・ tomhさん、ハラギャーテイさん、kasamaさん、他