第412問の解答
問題[平面図形]
|
|
|
|
|
|
|
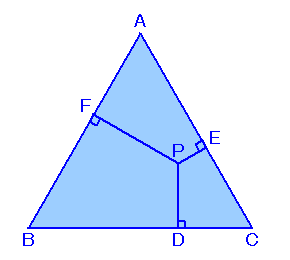 |
左図のような、高さが6cmである正三角形ABCがあります。 この三角形の内部(辺上は含みません)に点Pをとって、点Pから各辺に下ろした垂線の長さ(単位はcm)はすべて整数となりました。 では、このような点Pは△ABCの内部に何カ所あるでしょうか。 |
|
|
|
|
|
|
解答例1
トトロ@Nさん、長野 美光さん、あ〜く@ぴかぴかの(略さん、DrKさん、uchinyanさん、P・Kマニアさん、n厨さん、小西孝一さん、スモークマンさん、M.Hossieさん、しゅさん、他
正三角形ABCの1辺の長さをaとします。
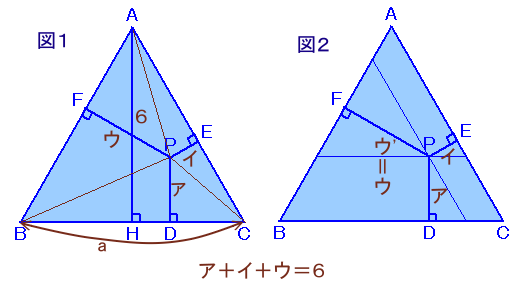
題意を満たす点Pに対して、(図1)
△ABC=△PBC+△PCA+△PABより、
1/2×a×6=1/2×a×ア+1/2×a×イ+1/2×a×ウよって、
ア+イ+ウ=6 ・・・ (1)
となります。(ただし、点Pは辺上にはないことから、ア、イ、ウ>0)逆に、(1)が成り立つようなア、イ、ウ>0となる整数に対して、 (図2)
辺BCと平行でBCとの距離がアとなる直線と 、辺CAと平行でCAとの距離がイとなる直線の交点をPとし、Pから各辺に下ろした垂線の足をD、E、Fとします。このとき、PD=ア、PE=イとなっています。
さて、PF=ウ’とすると、先ほどと同様にして、
ア+イ+ウ’=6 ・・・ (2)よって、ウ=ウ’となり、点Pは題意を満たすことが分かります。
以上から、題意を満たす点Pの個数は、(1)を満たす正の整数ア、イ、ウの組み合わせの個数と一致することになります。
さてこれらは、
ア=1のとき、(イ、ウ)=(1、4)、(2、3)、(3、1)、(4、1) ・・・ 4個
ア=2のとき、(イ、ウ)=(1、3)、(2、2)、(3、1) ・・・ 3個
ア=3のとき、(イ、ウ)=(1、2)、(2、1) ・・・ 2個
ア=4のとき、(イ、ウ)=(1、1) ・・・ 1個よって、
合計=4+3+2+1=10個
と求まります。答: 10カ所
以上
解答例2
辻。さん、みかんさん、CRYING DOLPHINさん、tomhさん、トトロ@Nさん、なかさん、kasamaさん、きょろ文さん、カケルさん、他
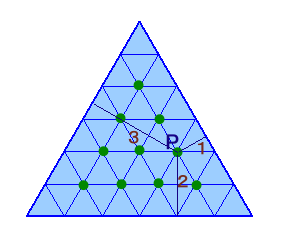
点Pは上図のように各辺と平行で距離が1〜5cmの直線の交点となることから、
正三角形ABCの6×6=36等分した小さな正三角形の頂点になります。これらで、正三角形ABCの内部にあるものは(辺上を除く)、
1+2+3+4=10個
あることが分かります。