第413問の解答
問題[平面図形]
|
|
|
|
|
|
|
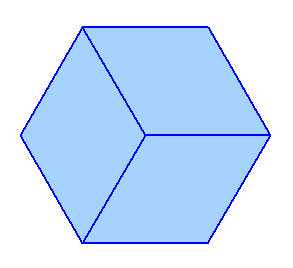 |
左図は、正六角形を3つの菱形で分割したところを表しています。 同じようにして、正16角形を菱形で分割することにします。菱形の個数が最も少なくなるようにするとき、その個数を求めてください。 ただし、菱形の一辺の長さはすべて正16角形の一辺の長さと等しいものとします |
|
|
|
|
|
|
解答例1
姉小路さん、uchinyanさん、拓パパさん、takaisaさん、まるケンさん、あ〜く@ぴかぴかの(略さん、なかさん、ゴンともさん、ミミズクはくず耳さん、始 受験勉強君さん、うのたかはるさん、他
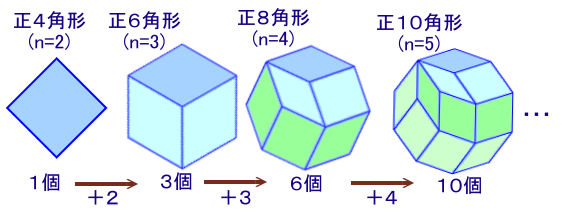
正2n角形(2≦n≦5)のときの個数をFnとして考えてみます。
正4角形(n=2)のとき ・・・ 1個
正6角形(n=3)のとき ・・・ 3個(+2)
正8角形(n=4)のとき ・・・ 6個(+3)
正10角形(n=5)のとき ・・・ 10個(+4)
と、増分が1ずつ増えていきます。
よって、Fn−Fn-1=nとなることから、
一般式は、Fn=Σ(k=1..n-1)k=n(n-1)/2
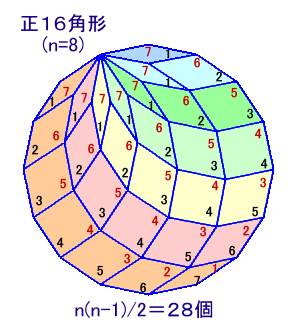
とくに本問ではF8=8×7/2=28個と予想されます実際、下記例では正16角形を菱形28個で分割できています。
なお、この解法では28個が最も少ない個数であることは示されていません。
答: 28個
以上
解答例2
なかさん、uchinyanさん、算太郎さん他
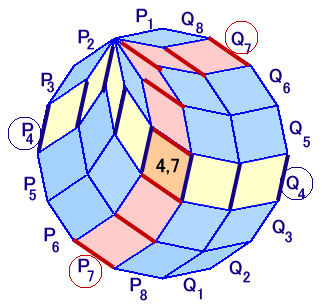
正16角形の辺をP1、P2、・・・、P8およびQ1、Q2、・・・、Q8と名前をつけます。
すると、 P1とQ1、P2とQ2、・・・、P8とQ8は、それぞれ向かい合っており平行です。
今、正16角形がN個の菱形で分割できたと仮定し、N=28を示してみましょう。
(解答例1から、少なくとも1通りは分割する方法があることが分かります。)そこで、P1、P2、・・・、P8の中から任意の辺Piを選びます。
すると、Piをちょうど辺とするような菱形が存在するはずです。
また、この菱形でPiの対辺を辺とするような菱形が存在、・・・・、というように、
次々と帯状につながる菱形の連鎖Ciを考えると、これらの最後は正16角形のある辺と一致しますが、
これらの菱形の対辺が全て平行であることから、最後の辺はQiに一致するはずです。今度は、辺Pk(ただし、i≠k)について同様な連鎖Ckを考えると、
連鎖Ciと連鎖Ckはどこかで交差するはずです。
そして、交差した個所の菱形は、辺Piに平行な2辺と、辺Pkに平行な2辺からできています。
(上図の例では、i=4、k=7)以上のようにして、P1、P2、・・・、P8の中から任意の異なる2辺PiとPkに対し、
分割した菱形のうちのある1個を対応させることができます。逆に分割した菱形のうちの任意の1個を選び、2組の対辺に対してそれぞれ外側につながる菱形の連鎖を考えると、最後は正16面体の辺で、元の菱形の対辺に平行な2組の辺に到達します。
また、この2組の辺の一方はP1、P2、・・・、P8の中の異なる2辺PiとPkに一致するはずです。さらに、PiとPkの組み合わせが異なると、対辺の一方は平行でないことから対応する菱形は異なります。
従って、分割した菱形の個数は、8個の辺P1、P2、・・・、P8の中から2組の辺を選ぶ選び方、すなわち8C2=28となることが分かります。
なお、同様にして一般に正2n角形のときは、菱形の個数はnC2=n(n-1)/2となることが分かります。