第４１５問の解答

問題［場合の数］

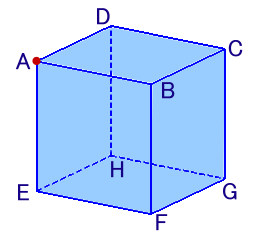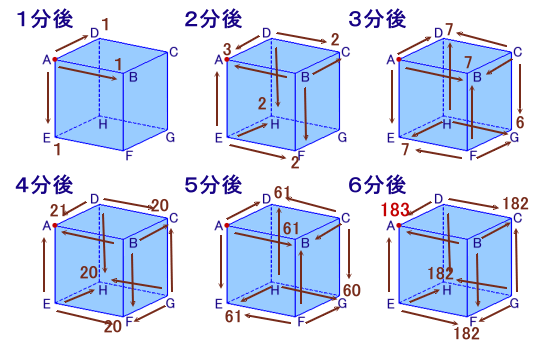
左図のような立方体ＡＢＣＤ－ＥＦＧＨがあります。

いま、頂点Ａにテントウムシがいます。このテントウムシは、１分ごとに隣り合ういずれかの頂点に移動します。（例えば、頂点Ａにいる場合は、１分後にＢ、Ｄ、Ｅのいずれかの頂点に移動）

では、６分後にテントウムシが頂点Ａにいるような移動方法は何通りあるでしょうか。

解答例１

トトロ＠Ｎさん、みかんさん、N.Nishiさん、CRYING DOLPHINさん、キノピーさん、ゆんななこさん、萬田銀次郎さん、TODAIJI 1-Cさん、他

　１分ごとに、各頂点への移動方法の数を書いていくと上図のようになります。
　

答：　１８３通り

以上

解答例２

Taroさん、uchinyanさん、tomhさん、他

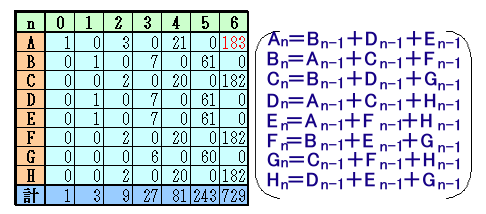
n分後の各頂点への移動方法の数をA_n、B_n、・・・、H_nとし、漸化式を求めて計算すると上表のようになります。本問では、A₆＝１８３通りとなります。

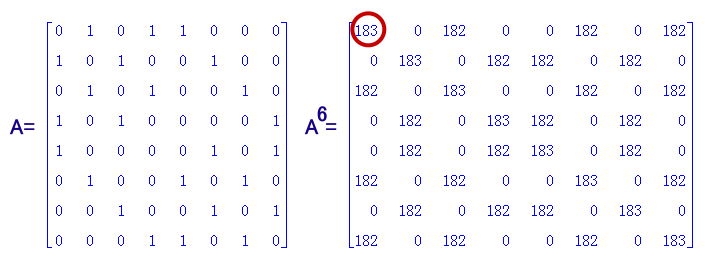
（参考）行列で計算することもできます。

解答例３

なかさん、長野　美光さん、ミミズクはくず耳さん、他

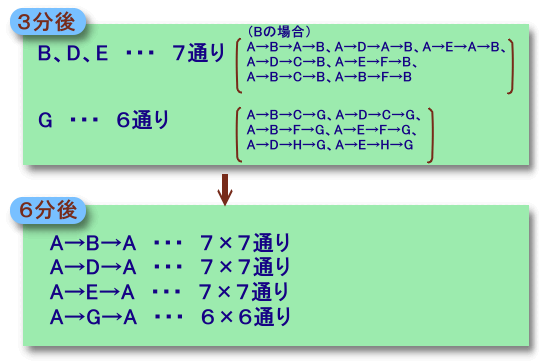
３分後には、B、D、E、またはGのいずれかにいて、
　B、D、Eへは７通り、Gへは６通り。

６分後には、それぞれ往復することになるので、
　７×７＋７×７＋７×７＋６×６＝１８３通り。

解答例４

小学名探偵さん、他

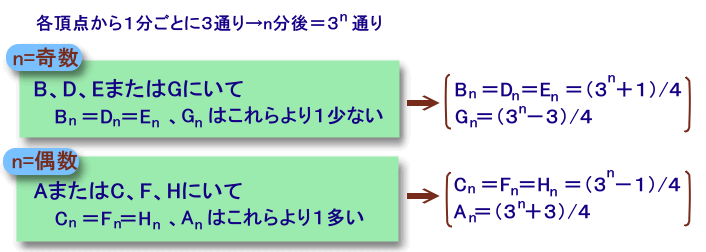
n分後について、奇数のときと偶数のときで上記事項が成り立ちます。（帰納法にて証明できる）

n＝奇数のとき：（B_n＋D_n＋E_n＋G_n）＝３ⁿ
→B_n＝D_n＝E_n＝（３ⁿ＋１）/４、G_n＝（３ⁿ－３）/４

n＝偶数のとき：（A_n＋C_n＋F_n＋H_n）＝３ⁿ
→C_n＝F_n＝H_n＝（３ⁿ－１）/４、A_n＝（３ⁿ＋３）/４

とくに本問では、A₆＝（３⁶＋３）/４＝（７２９＋３）/４＝１８３通りとなります。

（その他の解法）

何回Aに戻るかで場合分け　・・・　あ～く＠ぴかぴかの（略さん、他
　

A からの距離により (B,D,E) , (C,F,H) , (G) の３グループに分け数える　・・・　つよしさん、他
　

立方体の3辺に沿っての移動に着目　・・・　uchinyanさん、他
　

２分後ごとの移動に着目　・・・　工事中さん、他
　

樹形図で計算する　・・・　始受験勉強君さん、ゴンともさん、築さん、他
　

プログラムで計算する　・・・　kasamaさん、他
　