第４１６問の解答

問題［平面図形］

問題図

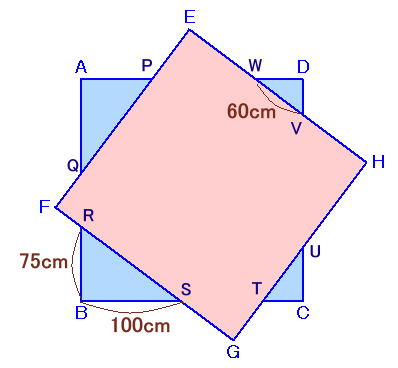左図のように、同じ大きさの正方形の紙を２枚重ました。

すると、図のように、ＲＢ＝７５cm、ＢＳ＝１００cm、ＶＷ＝６０cmとなりました。

このとき、この正方形の一辺の長さを求めてください。

解答例１

CRYING DOLPHINさん、ｎ厨さん、数楽者さん、あ〜く＠ぴかぴかの（略さん、uchinyanさん、ほげさん、姉小路さん、ミミズクはくず耳さん、N.Nishiさん、 他

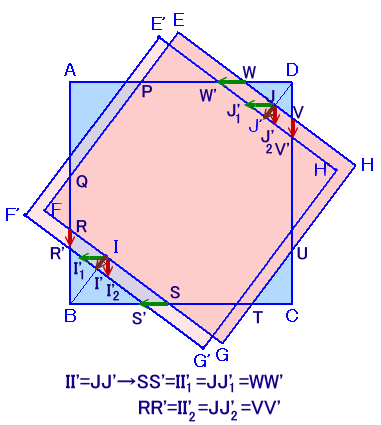
（補題１）合同な２つの正方形が重なった部分が八角形のとき、向かい合う辺の長さ の和（例えば、ＲＳ＋ＷＶ）は、一定値である。

（証明）正方形ＥＦＧＨが平行移動したものをＥ'Ｆ'Ｇ'Ｈ'とします。

参考図1-1

辺ＥＨおよび辺ＦＧの移動量は同じなので、ＥＨとＥ'Ｈ'、ＦＧとＦ'Ｇ'の距離は等しい。

従って、
ＤからＥＨおよびＥ'Ｈ'に下ろした垂線の足をＪおよびＪ'、
またＤからＥＨおよびＥ'Ｈ'に下ろした垂線の足をＪおよびＪ'とすると、
ＪＪ'とＩＩ'は、平行でかつ長さが等しくなります。　・・・　（１）

ＪJ'1とＷＷ'が平行、ＪJ'2とVV'が平行となるようなJ'1およびＪ'2を辺Ｅ'Ｈ'に取ります。
すると、ＷＷ'J'1ＪおよびJ'2ＪV'Vは平行四辺形なので、
　ＪJ'1＝ＷＷ'、ＪJ'2＝VV'となります。

全く同様に、ＩＩ'1＝ＳＳ'、ＩＩ'2＝ＲＲ'となります。

従って（１）より、
　ＷＷ'＝ＳＳ'、VV'＝ＲＲ'、J'1J'2＝Ｉ'1Ｉ'2　・・・　（２）
となります。

Ｗ'V'−ＷＶ＝J'1J'2、ＲＳ−Ｒ'Ｓ'＝Ｉ'1Ｉ'2　となることから、
（２）より、Ｗ'V'−ＷＶ＝ＲＳ−Ｒ'Ｓ'

よって、
　ＲＳ＋ＷＶ＝Ｒ'Ｓ'＋Ｗ'V'
となります。

他の辺についても同様。

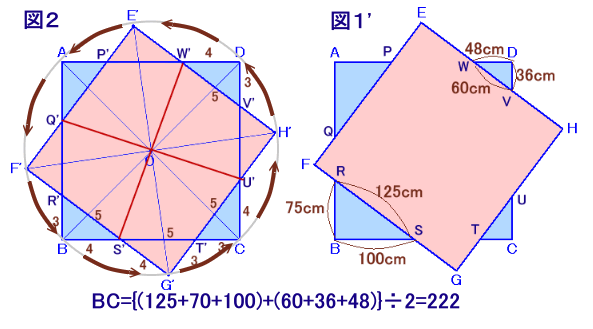
（補題２）合同な２つの正方形の中心を一致させて斜めに重ねると、重なった部分は辺の長さが全て等しい八角形とな り、重なっていない部分は全て合同な直角三角形となる。

（証明）正方形ＥＦＧＨの中心Ｏを中心に回転したものをＥ'Ｆ'Ｇ'Ｈ'とします。これはＥＦＧＨを平行移動し、中心がＯと一致するようにしたもにに同じです。（図２）

参考図1-2

対称性から８つの直角三角形Ｐ'ＡＱ'、Ｑ'ＢＲ'、・・・、Ｗ'ＥＰ'は全て合同となります。（少しおおざっぱですが）

問題図でＲＢＳは辺の長さが３：４：５の直角三角形より、
これと相似なＶＤＷ等も同じく辺の長さが３：４：５の直角三角形。

よって、図１より、残りの辺は、
　ＲＳ＝１００cm×５/４＝１２５cm、
　ＷＤ＝６０cm×４/５＝４８cm、ＤＶ＝６０cm×３/５＝３６cm
と分かります。

補題１より、ＲＳ＋ＷＶ、ＲＢ＋ＤＶ、ＢＳ＋ＷＤは、それぞれ一定だから
　Ｒ'Ｓ'＝W'V'＝（ＲＳ＋ＷＶ）×１/２＝（１２５＋６０）×１/２
　Ｒ'Ｂ＝ＤV'＝（ＲＢ＋ＤＶ）×１/２＝（７５＋３６）×１/２
　ＢＳ'＝W'Ｄ＝（ＢＳ＋ＷＤ）×１/２＝（１００＋４８）×１/２

よって、
　ＢＣ
＝ＢＳ'＋S'T'＋T'C
＝ＢＳ'＋Ｒ'S'＋Ｒ'Ｂ
＝｛（１２５＋７５＋１００）＋（６０＋３６＋４８）｝×１/２
＝（３００＋１４４）÷２＝２２２cm
と求まります。

答：　 ２２２cm

以上

解答例２

なかさん、ごんごんまさん、万打無さん、 他

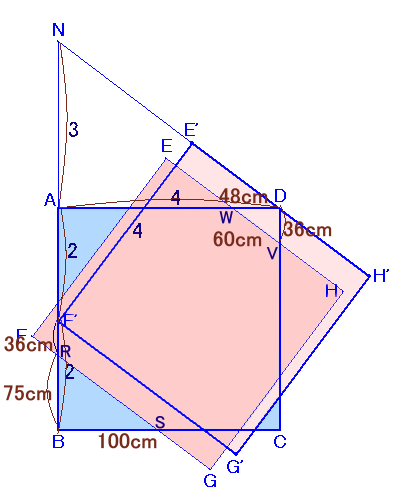
正方形ＥＦＧＨを平行移動して、Ｆが辺ＡＢ上に、Ｄが辺ＥＨに来るようにしたものをＥ'Ｆ'Ｇ'Ｈ'とし 、
ＢＡとＨ'Ｅ'の延長線の交点をＮとします。

参考図２

解答例１の補題１証明と同様にして、
　Ｆ'Ｒ＝ＤＶ＝３６cmより、Ｆ'Ｂ＝７５＋３６＝１１１cm。

△ＮＡＤ、△ＮＥ'Ｆ'は△ＲＳＢと相似より、辺の長さが３：４：５の直角三角形。
従って、正方形の１辺の長さを４とすると、
　ＮＦ'＝５、ＮＡ＝３
よって、ＡＦ'＝５−３＝２、Ｆ'Ｂ＝４−２＝２。

ＡＦ'＝１１１cmより、
　ＡＢ＝１１１×２＝２２２cm
と求まります。

（その他の解法）