第４１７問の解答

問題［平面図形］

問題図

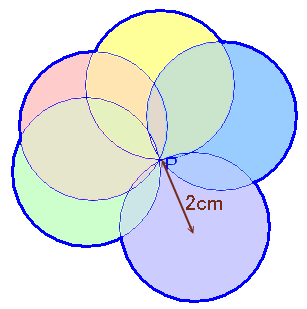
左図のように、半径が２cmの円を５つ、すべて点Ｐを通るように描きました。

この図形の周の長さ（図の太線の部分の長さ）を求めてください。

解答例１

姉小路さん、DrKさん、始 受験勉強君さん、CRYING DOLPHINさん、なかさん、M.Hossieさん、さいと散さん、 他

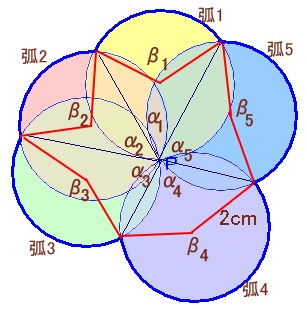
５個の円について、求める図形を形成している弧を、弧1、弧2、・・・、弧5とします。

参考図１


それぞれの弧に対する円周角、中心角を、それぞれα1、α2、・・・、α5およびβ1、β2、・・・、β5とします。

β1＝α1×２、β2＝α2×２、・・・、β5＝α5×２、および
α1＋α2＋・・・＋α5＝３６０°より、
β1＋β2＋・・・＋β5＝３６０°×２

よって、
　弧1＋弧2＋・・・＋弧5
＝３．１４×４cm×２×（β1＋β2＋・・・＋β5）÷３６０°
＝３．１４×４cm×２×２
＝２５．１２cm
と求まります。

答：　 ２５．１２cm

以上

解答例２

トトロ＠Ｎさん、uchinyanさん、長野　美光さん、 みっちん。HCR32改さん、tomhさん、アヒーのおじさんさん、うのたかはるさん、K.N.I.F.E.さん、他

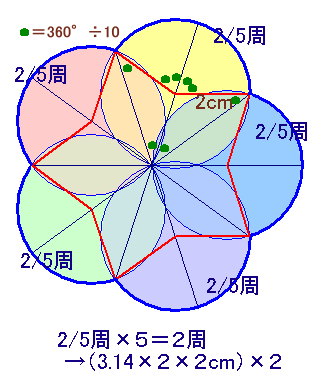
５つの円が等間隔に並んでいる場合を想定して求めてみます。

参考図２

すると、それぞれの弧に対する中心角は、３６０°÷１０×４＝１４４°になります。
従って、中心角の合計は、１４４°×５＝７２０°＝３６０°×２。

よって、求める長さは、ちょうど半径２cmの円周の２倍となります。
以下、同様。