第４２０問の解答

問題［場合の数］

１～６の数字が書かれたカードが１枚ずつ、全部で６枚あります。これらのカードを並べて、次の条件に当てはまるような６ケ
タの整数を作ることにします。何通り作れるでしょうか？

　　　　（条件）どの位の数についても、その左側にはその数よりも大きな数は２個以下しかない。

解答例１

アヒーのおじさんさん、始受験勉強君さん、みかんさん、CRYING DOLPHINさん、りえパパさん、tomhさん、uchinyanさん、小西孝一さん、DrKさん、ドイルさん、鉄腕アトムでーすさん、M.Hossieさん、Hollyさん、しんちゃんさん、他多数

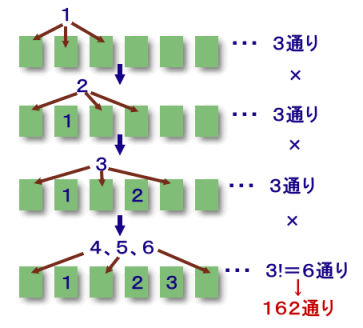
１から順に数字を置いてみます。

１の数字：左から１～３桁の３個所に置ける　・・・　３通り
　

２の数字：１を除く左から１～３桁の３個所に置ける　・・・　３通り
　

３の数字：１、２を除く左から１～３桁の３個所に置ける　・・・　３通り
　

４、５、６の数字：これらより大きい数字は２個以下なので、残り３個所に自由に置ける　・・・　３!＝６通り

従って、
　合計＝３×３×３×６＝１６２通り
と求まります。

答：　１６２通り

以上

解答例２

nobuさん、数楽者さん、スモークマンさん、他

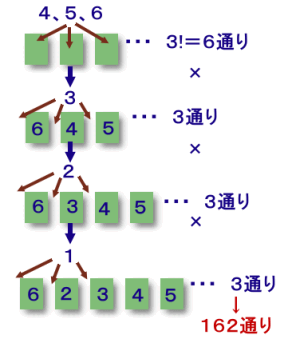
解答例１と逆に数字の大きい順に置いてみます。

４、５、６の数字：これらより大きい数字は２個以下なので、３個所に自由に置ける　・・・　３!＝６通り
　

３の数字：最初の２桁の数字の前後、計３個所に置ける　・・・　３通り
　

２の数字：最初の２桁の数字の前後、計３個所に置ける　・・・　３通り
　

１の数字：最初の２桁の数字の前後、計３個所に置ける　・・・　３通り

従って、
　合計＝６×３×３×３＝１６２通り
と求まります。

解答例３

おかひで博士さん、すてっぷさん、ほげさん、uchinyanさん、他

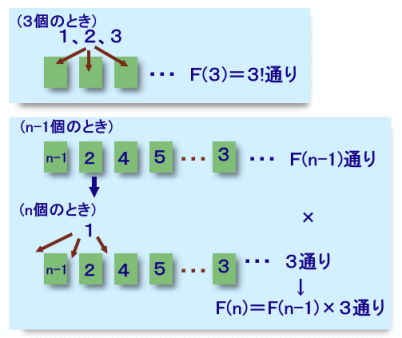
n桁の数字のうち、条件を満たす整数の個数をF(n)とし、漸化式で考えます。

n＝１～３のとき：各桁の数字とも、それより大きい数字は２個以下なので、n個所に自由に置ける
　・・・　n!通り　→　F(n)＝n!
　

n＞３のとき：最初の２桁の数字の前後、計３個所に置ける　
・・・　３通り　　→　F(n)＝３×F(n-1)

従って、n＞３では等比数列になり、
　F（n）＝３^n-3×F（３）＝３^n-3×６＝３^n-2×２
となります。

とくに、n＝６とすれば、
　本問の答え＝３^6-2×２＝１６２通り
と求まります。

解答例４

小学名探偵さん、トトロ@Nさん、他

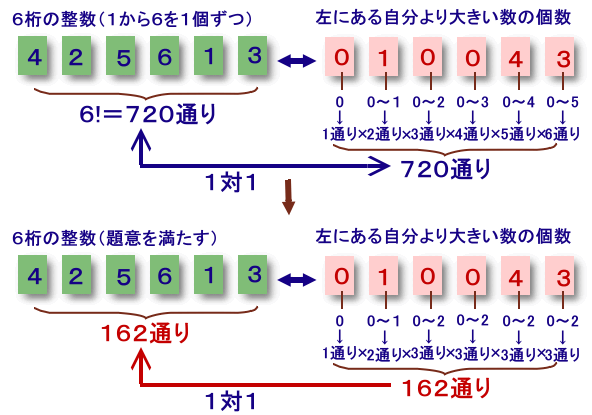
６桁の整数に対し、「各桁の数字について『左にある自分より大きい数字の個数』を並べた整数」（「大きい数字個数数」と呼ぶことにします）を対応させることにします。
例えば、４２５６１３の場合、
　・１桁目の４：左に大きい数字なし　・・・　０個
　・２桁目の２：左に大きい数字は４のみ　・・・　１個
　・３桁目の５：左に大きい数字なし　・・・　０個
　・４桁目の６：左に大きい数字なし　・・・　０個
　・５桁目の１：左に大きい数字は４、２、５、６　・・・　４個
　・６桁目の３：左に大きい数字は４、５、６　・・・　３個
となり０１００４３が対応します。

さて、６桁の整数のうち、１から６までの数字を１個ずつ並べたものは、全部で６!＝７２０通りあります。

また、大きい数字個数数については、
　・１桁目：左に大きい数字なし　・・・　１通り
　・２桁目の２：左に大きい数字は０～１個　・・・　２通り
　・３桁目の５：左に大きい数字は０～２個　・・・　３通り
　・４桁目の６：左に大きい数字は０～３個　・・・　４通り
　・５桁目の１：左に大きい数字は０～４個　・・・　５通り
　・６桁目の３：左に大きい数字は０～５個　・・・　６通り
となり、全部で１×２×３×４×５×６＝６!＝７２０通りあります。

従って、「６桁の整数のうち、１から６までの数字を１個ずつ並べたもの」と、これらに対する「大きい数字個数数」は、１対１に対応することがわかります。

さて、題意の条件（どの位の数についても、その左側にはその数よりも大きな数は２個以下しかない。）を満たすような６桁の整数について、対応する大きい数字個数数は、
　・１桁目：左に大きい数字なし　・・・　１通り
　・２桁目の２：左に大きい数字は０～１個　・・・　２通り
　・３桁目の５：左に大きい数字は０～２個　・・・　３通り
　・４桁目の６：左に大きい数字は０～２個　・・・　３通り
　・５桁目の１：左に大きい数字は０～２個　・・・　３通り
　・６桁目の３：左に大きい数字は０～２個　・・・　３通り
となり、全部で１×２×３×３×３×３＝１６２通りあります。

よって、題意を満たすような６桁の整数も、１６２通りあることが分かります。

（その他の解法）

プログラムで数え上げる　・・・　なかさん、ハラギャーテイさん、kasamaさん、他
　

場合分けして数え上げる　・・・　姉小路さん、ゴンともさん、N.Nishiさん、他
　

条件に合わないものを除く　・・・　ハッスル　ハッスルさん、他
　

確率から求める　・・・　カーリッジさん、他
　


	６桁の整数に対し、「各桁の数字について『左にある自分より大きい数字の個数』を並べた整数」（「大きい数字個数数」と呼ぶことにします）を対応させることにします。例えば、４２５６１３の場合、　・１桁目の４：左に大きい数字なし　・・・　０個　・２桁目の２：左に大きい数字は４のみ　・・・　１個　・３桁目の５：左に大きい数字なし　・・・　０個　・４桁目の６：左に大きい数字なし　・・・　０個　・５桁目の１：左に大きい数字は４、２、５、６　・・・　４個　・６桁目の３：左に大きい数字は４、５、６　・・・　３個となり０１００４３が対応します。さて、６桁の整数のうち、１から６までの数字を１個ずつ並べたものは、全部で６!＝７２０通りあります。また、大きい数字個数数については、　・１桁目：左に大きい数字なし　・・・　１通り　・２桁目の２：左に大きい数字は０～１個　・・・　２通り　・３桁目の５：左に大きい数字は０～２個　・・・　３通り　・４桁目の６：左に大きい数字は０～３個　・・・　４通り　・５桁目の１：左に大きい数字は０～４個　・・・　５通り　・６桁目の３：左に大きい数字は０～５個　・・・　６通りとなり、全部で１×２×３×４×５×６＝６!＝７２０通りあります。従って、「６桁の整数のうち、１から６までの数字を１個ずつ並べたもの」と、これらに対する「大きい数字個数数」は、１対１に対応することがわかります。さて、題意の条件（どの位の数についても、その左側にはその数よりも大きな数は２個以下しかない。）を満たすような６桁の整数について、対応する大きい数字個数数は、　・１桁目：左に大きい数字なし　・・・　１通り　・２桁目の２：左に大きい数字は０～１個　・・・　２通り　・３桁目の５：左に大きい数字は０～２個　・・・　３通り　・４桁目の６：左に大きい数字は０～２個　・・・　３通り　・５桁目の１：左に大きい数字は０～２個　・・・　３通り　・６桁目の３：左に大きい数字は０～２個　・・・　３通りとなり、全部で１×２×３×３×３×３＝１６２通りあります。よって、題意を満たすような６桁の整数も、１６２通りあることが分かります。