第421問の解答
問題[空間図形]
|
|
|
|
|
|
|
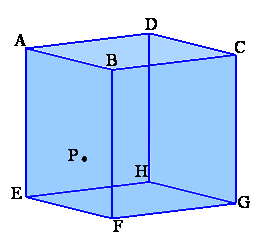 |
左図のような一辺の長さが12cmの立方体ABCD−EFGHがあります。点Pは立方体の内部にある点で、 いま、点Pと立方体の各面について対称な点をとります。(全部で6つできますね) これらの6つの点を結んでできる立体と、もとの立方体の重なった部分の体積を求めてください。 |
|
|
|
|
|
|
解答例1
Taroさん、姉小路さん、tomhさん、DrKさん、なかさん、n厨@眠さん、小西孝一さん、頑張れ松井&ヤンキースさん、きょろ文さん、uchinyanさん、他
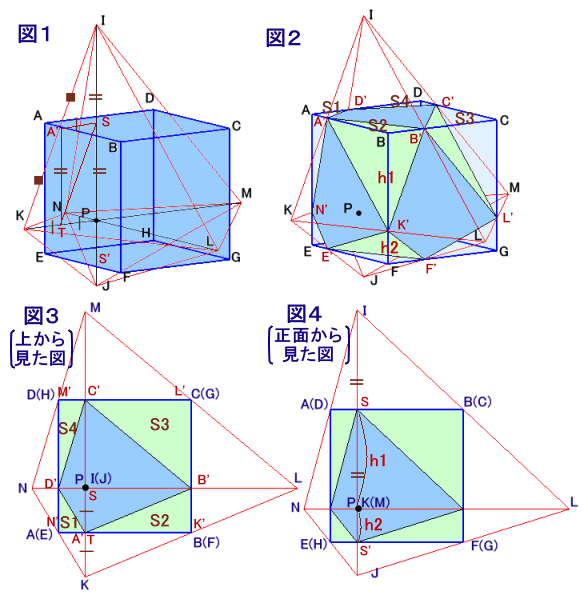
点Pと立方体(1辺の長さをaとします。a=12cm)の各面について対称な点を、I、J、K、L、M、Nとします。 (図1)
IPの中点をS、KPの中点をTとすると、題意より、
Sは上面ABCD上に、Tは側面AEFB上にあることが分かります。そこで、IKの中点をA'とすると、△IKPに関して、中点連結定理より、
A'SはKPと平行、A'TはIPと平行となります。従って、A'は上面ABCD上かつ側面AEFB上にあることになるので、
実は辺AB上にあることが分かります。同様にして、IL、IM、INの中点をB'、C'、D'、およびJK、JL、JM、JNの中点をE'、F'、G'、H’とすると、
B'、C'、D'は、それぞれ辺BC、CD、DA上に、E'、F'、G'、H’は、辺EF、FG、GH、HE上にあることが分かります。よって、I、J、K、L、M、Nを結んでできる立体は八面体になりますが、
それぞれの面が元の立方体の8隅を切断し、8個の三角錐を切り落とすことになります。上4個の三角錐の底面と、下4個の三角錐の底面は、それぞれ合同となります。
これらの面積をS1、S2、S3、S4とすると、
S1+S2+S3+S4=正方形ABCD×1/2=a2×1/2
となります。また、三角錐の高さは、上4個、下4個でそれぞれ等しく、これらをh1、h2とすると、
h1+h2=AE=a
となります。よって、
8個の三角錐体積合計
=1/3×(S1+S2+S3+S4)×h1+1/3×(S1+S2+S3+S4)×h2
=1/3×(S1+S2+S3+S4)×(h1+h2)
=1/3×a2×1/2×a
=1/6×a3従って、
求める体積
=a3−1/6×a3
=5/6×a3
=5/6×123
=1440cm3
と求まります。答: 1440cm3
以上
解答例2
アヒーのおじさんさん、みかんさん、 他
解答例1と逆に八面体からはみ出た6個の四角錐の体積を除いて求めます。(図は解答例1を参照)
八面体を上下2つの四角錐に分割すると、共通する底面積はa2×2で、高さの和はa×2、
よって、体積=1/3×(2×a2)×(2×a)=4/3×a3また、6個の四角錐の底面積は、いずれもa2×1/2で、向かい合う四角錐の高さの和はaとなるので、
体積合計=(1/3×a2×1/2×a)×3=1/2×a3=5/6×a3
となり、以下同様。
(その他の解法)
CADで作図して体積を計算 ・・・ kasamaさん、 他
数式処理ソフトを使って計算 ・・・ ゴンともさん 他