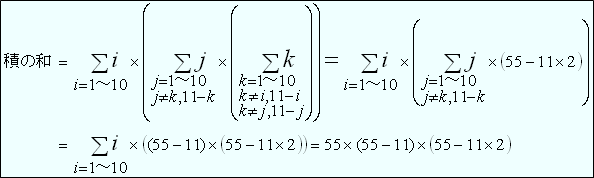第422問の解答
問題[場合の数]
|
|
|
|
|
|
1から10までの数の書かれたカードが1枚ずつ、合計10枚あります。 このような取り出し方全てについて、3枚のカードに書かれた数の積(3つの数をかけ算したもの)を求め、紙にメモしていきま では、紙にメモされた数の合計はいくつでしょうか。 |
|
|
|
|
|
解答例1
はなうさん、uchinyanさん、他
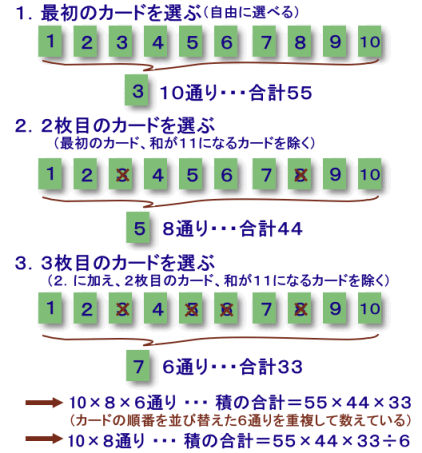
1枚目のカード:自由に選べる ・・・ 10通り、合計55
2枚目のカード:1枚目および1枚目との和が11になるカード以外 ・・・ 8通り、合計=55−11=44
3枚目のカード:1枚目および1枚目との和が11になるカード、2枚目および2枚目との和が11になる カード
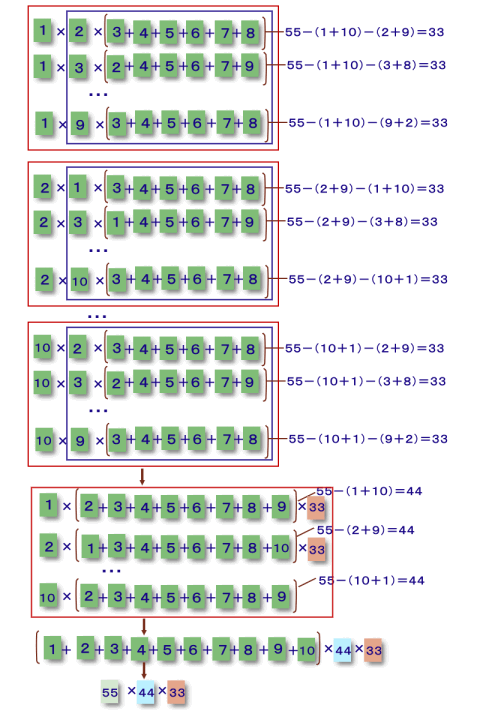
・・・ 6通り、合計=55−11−11=33そこで、これらの積の合計を下図のようにして数えてみます。
最初のカードと2枚目のカードを選んだとき、3枚目のカードの和は、常に55−11×2=33。
よって、積和は、最初のカードと2枚目のカードの積の和に33を掛けたものに等しい。また、1枚目のカードを選んだとき、2枚目のカードの和は、常に55−11=44、
従って、積和は、1枚目のカードの和(55)に44と33を掛けたものに等しい。ただし、これらの和は、カードを選ぶ順番を変えたときの6通りを重複して数えているので、
求める積和は、55×44×33÷6=13310と求まります。
答: 13310
以上
(参考)式で積和を表したとき(重複分を含む)
解答例2
LAR-menさん、ごんごんまさん、アヒーのおじさんさん、ぽんさん、水田Xさん、ほげさん、他
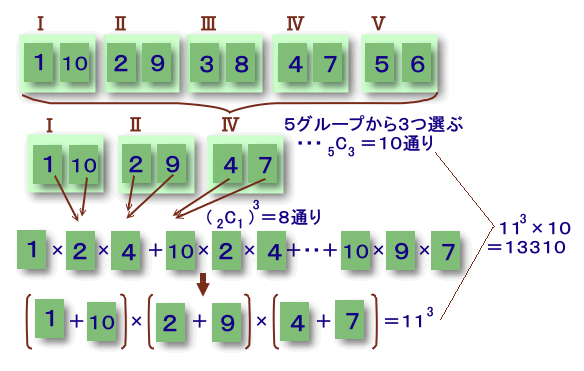
10枚のカードを、和が11となる2枚ずつの5グループに分けて考えると、
「3枚のうちどの2枚を選んでも、その合計は11にならない」ような3枚を取り出す
ということは、
5グループから3グループを選び、それらからカードを1枚ずつ取り出す
ことと同等であることが分かります。まず、5グループから3グループを選ぶ方法は、5C3=5!/(3!2!)=10通りあります。
次に選んだ3グループのそれぞれからカードを1枚ずつ選ぶ方法は、(2C1)2=8通りあり、
それらの積の和は、各グループのカードの和(いずれも11)の積に等しくなります。従って、
積の合計=113×10=13310通り
と求まります。
(その他の解法)
全てのケースから題意を満たさない場合の積和を除いて求める ・・・ omegaさん、あ〜く@ぴかぴかの(略さん、CRYING DOLPHINさん、姉小路さん、uchinyanさん、他
プログラムで計算 ・・・ tomhさん、トトロ@Nさん、Taroさん、オモシロ※※館館長「影」さん、ハラギャーテイさん、kasamaさん、小西孝一さん、ねるとんさん、なかさん、他
全て書き出して計算 ・・・ uchinyanさん 、みかんさん 、ゴンともさん 、N.Nishiさん 、M.Hossieさん 、Hollyさん 、大岡 敏幸さん 、 他