第４２４問の解答

問題［平面図形、規則性］

問題図

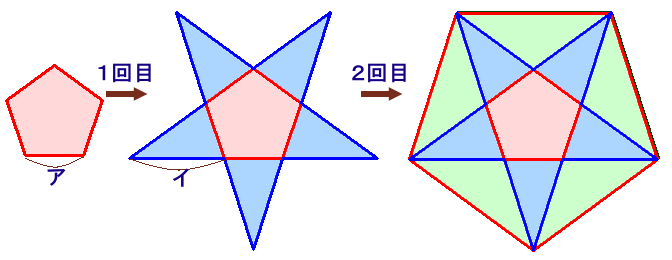
上図のような、一辺の長さがアcmである正５角形があります。
この正５角形の各辺を延長すると、図のような星形ができ、その一辺の長さをイcmとします。（１回目の作業）
次に、星形の鋭角の頂点を結ぶと、正５角形ができます。（２回目の作業）

以下３回目以降の作業を繰り返すと、この図形は、
　　正５角形→星形→正５角形→星形→・・・
と変化します。

このとき、１０回目の作業後にできる正５角形の一辺の長さを　
　Ａ×ア＋Ｂ×イ　cm
と表すとき、Ａ、Ｂに当てはまる整数を答えてください。

解答例１

トトロ＠Ｎさん、あ〜く＠ぴかぴかの（略さん、uchinyanさん、始 受験勉強君さん、アヒーのおじさんさん、mhayashiさん、圭太さん、M.Hossieさん、小学名探偵さん、DrKさん、3秒の世界さん、emikoさん、はなうさん、N.Nishiさん、他

n回目の作業後にできる図形（正五角形または星形）の１辺の長さをdnとし、
dn＝pn×a＋qn×bとします（ただし、a＝アの長さ、b＝イの長さ）。

まず、d0＝a、d1＝bより、
 　d0＝p0×a＋q0×b＝a　→　（p0、q0）＝（１、０）
　 d1＝p1×a＋q1×b＝b　→　（p1、q1）＝（０、１） 　・・・　（１）
となります。

参考図１

次に、n≧２について、dnの漸化式を求めてみましょう。

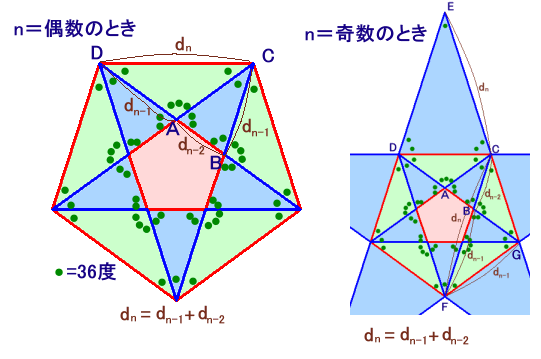
nが偶数のとき：
△CABと△DBCは、いずれも底角が７２度の二等点三角形となり相似。
また、△ACDは底角が３６度の二等辺三角形。

従って、
　DB＝DC＝dn、AD＝AC＝BC＝dn-1、AB＝dn-2
よって、
　dn＝dn-1＋dn-2
が成り立ちます。

nが奇数のとき：
△ADCと△FDCは、いずれも底角が７２度の二等点三角形で、底辺DCが共通なので合同。
また、△FGBも底角が７２度の二等辺三角形。

従って、
　FC＝EC＝dn、FB＝FG＝dn-1、BC＝dn-2
よって、
　dn＝dn-1＋dn-2
が成り立ちます。

以上から、nが偶数のときも、奇数のときも、
　dn＝dn-1＋dn-2　・・・　（２）
が成り立つことが分かります。

（２）より、
　dn＝（pn-1×a＋qn-1×b）＋（pn-2×a＋qn-×b）
　　＝（pn-1＋pn-2）×a＋（qn-1＋qn-2）×b

よって、
　pn＝pn-1＋pn-2、qn＝qn-1＋qn-2　・・・　（３）
が成り立ちます。（フィボナッチ数列）

従って、 （１）、（３）より、順次計算していくと、

参考図１−２

となり、
　A＝p10＝３４、
　B＝q10＝５５
と求まります。

答： 　A＝３４、B＝５５

以上

　

解答例２

tomhさん、ゴンともさん、kasamaさん、姉小路さん、スモークマンさん、他

参考図２


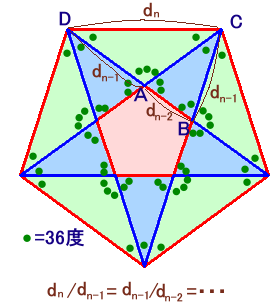
解答例１と同様に、△CABと△DBCが相似より、
　DC/BC＝BC/AB
よって、
　d1/d0＝d2/d1
が成り立ちます。

同様にして、　
　d2/d1＝d3/d2＝・・・
となることが分かります。

この値をｔとすると、
　dn＝tn×a　・・・　（１）
となります。（d0＝a）

三角関数を用いると、
　ｔ＝１/（２cos７２°）＝１/（２×（√５−１）/４））＝（√５＋１）/２
を得ます。

これは、（１）および解答例１の（２）より、
 t2×a＝t×a＋a
従って、
　t2−t−１＝0　　
を解いても得ることができます。　

（１）より、
　d10＝tn×a
　　＝{（√５＋１）/２}10×a
　　＝{（１２３＋５５√５）/２}×a
　　＝３４×a＋５５×（√５＋１）/２×a
　　＝３４×a＋５５×b
となります。　（d1＝t×a＝b）

従って、A＝３４、B＝５５と求まります。

（その他の解法）