第４２５問の解答

問題［推理］

マサルさん、トモエさん、ツヨシ君がそれぞれ監督を努めるサッカーチームがリーグ戦を行いました。

各チームは、それぞれ他チームと７試合ずつを行います。（１チームあたり１４試合）

順位の決定方法は、

  • 勝ったチームには、２点

  • 負けたチームには、０点

  • 引き分けたら、両チームに１点

を与える方法で計算し、勝ち点の最も多いチームを優勝とします。

全試合を終了して、勝ち点計算を行ったところ、ツヨシ君チームが優勝となりました。
ただし、勝った試合数が最も多かったのはトモエさんチーム、負けた試合が最も少なかったのはマサルさんチームであったそうです。
このとき、マサルさんチームの勝った試合数と勝ち点の合計を求めてください。

解答例１

ミキティさん、はなうさん、辻。さん、アヒーのおじさんさん、N.Nishiさん、M.Hossieさん、小学名探偵さん、uchinyanさん、姉小路さん、他

勝ち点合計＝４２点であることが、次のようにして分かります。

  • 勝ち試合数の合計＝負け試合数の合計

  • あるチームについて、勝ち試合数＝W、負け試合数＝Lとすると、
    引き分け試合数＝１４−W−L
    勝ち点    ＝W×２＋（１４−W−L）＝１４+（W−L)

  • したがって、 各チームの勝ち点合計＝１４×３ ＝４２点

通常は、勝ち試合数が最大、負け試合数が最小のチームが優勝します。

本問のような状況になるのは、

  • ３チームの勝ち点が極めて接近している。

  • ツヨシ君は、トモエさんより勝ち試合数が少ないのに勝ち点が多いので、引き分けが多い。

  • マサルさんは、負け試合数が最も少ないのに優勝できないので、引き分けがツヨシ君よりも多い。

などが考えられます。

そこで、３人の勝ち点が１５点（ツヨシ君）、１４点、１３点となるものと仮定し、上記状況を想定して試行錯誤すると、次のような２ケースが見つかります。

参考図１

答： 　１勝、勝ち点１３　または　２勝、勝ち点１４

以上

　

解答例２

すてっぷさん、他

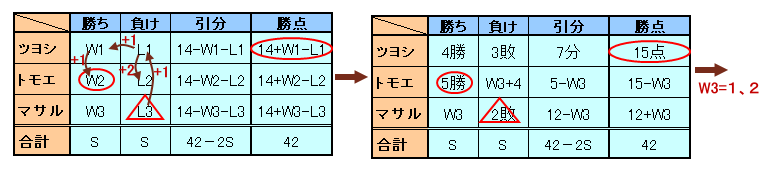
３人の試合結果を、ツヨシ君＝W１勝L１敗、トモエさん＝W２勝L２敗、マサルさん＝W３勝L３敗と、
また、勝ち数合計＝負け数合計＝Sとします。（下表）

参考図２

勝ち点はツヨシ君が最大だから、平均より大きい。
　W１−L１＞（W１−L１）＋（W２−L２）＋（W３−L３）＝（W１＋W２＋W３）−（L１＋L２＋L３）＝０
よって、
　W１−L１≧１　・・・　（１）

また、W１−L１＞W２−L２より、
　L２−L１＞W２−W１＞０　（W２が最大）
よって、
　L２≧L１＋２≧L３＋３　（L３が最小）　・・・　（２）

従って、
　W１≧L１＋１≧L３＋２
　W２≧W１＋１≧L１＋２≧L３＋３　・・・　（ ３）

あるチームの勝ち試合数は、他２チームの負け試合数計以下なので、
　L３＋L１≧W２
よって、
　L３≧W２−L１≧２　　・・・　（４）

また、チームの引き分け試合数は、他２チームの引き分け試合数計以下なので、
　（１４−W１−L１）＋（１４−W２−L２）≧１４−W３−L３
よって、
　１４≧（W１＋W２＋W３）＋（L１＋L２＋L３）−（W３＋L３）×２
　　　＝S×２−（W３＋L３）

従って、
　７≧S−（W３＋L３）＝W１＋W２−L３　・・・　（ ５）
（３）より、
　７≧（L３＋２）＋（L３＋３）
よって、
　L３≦２　・・・　（６）

（４）、（６）より、
　L３＝２　・・・　（ ７）
となります。

（３）、（７）より、
　W１≧４
　W２≧５
となり、また（５）より、
　W１＋W２≦７＋L３＝９
となるので、
　W１＝４
　W２＝５　・・・　（ ８）
が得られます。

すると、（４）より、
　L１≧W２−L３＝５−２＝３
（１）より、
　L１≦W１−１＝４−１＝３
従って、
　L１＝３　・・・　（ ９）
となります。

さて、
　勝ち試合数計＝W１＋W２＋W３＝４＋５＋W３＝９＋W３
　負け試合数計＝L１＋L２＋L３＝３＋L２＋２＝５＋L２
これらは等しいので、
　L２＝W３＋４
となります。

従って、３人の引き分け試合数は、
　７、５−W３、１２−W３
よって、３人の勝ち点は、
　１５、１５−W３、１２＋W３　・・・　（１０）
となります。

勝ち点はツヨシ君が最大より、
　１５＞１５−W３、１５＞１２＋W３
よって、
　W３＝１または２
となります。

以上から、本問の解は解答例１のケース１、ケース２の２通りしかないことが分かります。

（その他の解法）