第429問の解答
問題[平面図形]
|
|
|
|
|
|
|
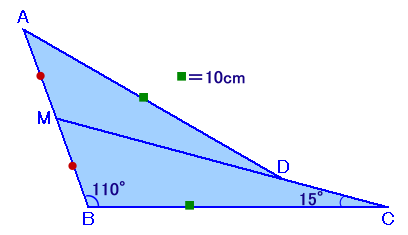 |
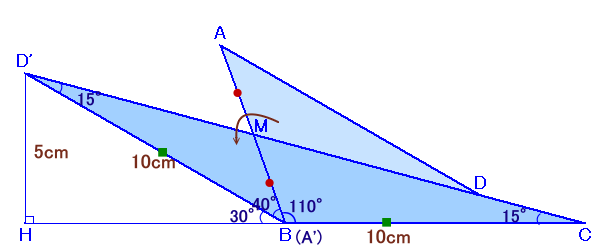
左図のような、BC=10cm、∠BCM=15度、∠MBC=110度の△MBCがあります。 いま、辺BMの延長上に、AM=BMとなるような点Aをとります。また、辺MC上に点Dをとったところ、AD=10cmとなりました。 このとき、この図形全体の面積(四角形ABCDの面積)を求めてください。 |
|
|
|
|
|
|
解答例1
mhayashiさん、みかんさん、uchinyanさん、トトロ@Nさん、アヒーのおじさんさん、CRYING DOLPHINさん、M.Hossieさん、N.Nishiさん、大岡 敏幸さん、他
点Mを中心にして△AMDを180°回転し、△A'MD'とします。
AM=MBより、点A'は点Bと一致します。
また、∠D'MB+∠BMC=∠DMA+∠BMC=180°、
従って、D'、M、Cは一直線上に並びます。BD'=AD=BC=10cmより、△MD'Cは二等辺三角形となります。
四角形ABCD=△AMD+△MBC=△BMD'+△MBC=△BD'Cとなります。
D'からCBの延長に下ろした垂線の足をHとすると、
∠D'BH=∠BD'C+∠BCD'=15×2=30°。
よって、
D'H=D'B×1/2=10×1/2=5cm。従って、
△BD'C=1/2×BC×D'H=1/2×10×5=25cm2
と求まります。答: 25cm2
以上
解答例2
あ〜く@ぴかぴかの(略さん、kazsyunさん、他
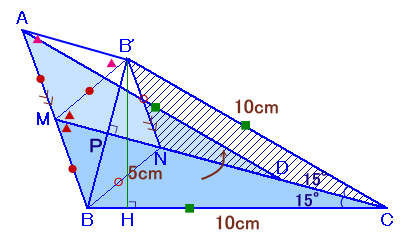
辺MCを軸に△MBCを折りかえしたものを△MB'Cとし 、B'を通りAMと平行に引いた直線とMCの交点をNとします。
△B'NCと△BNCは合同、
B'C=BC=10cm、B'N=BN、∠B'MC=∠BMC、∠B'CM=∠BCM=15°・・・ (1)
となります。
実は、△B'NCと△AMDが合同になることを証明していきましょう。MB'=MB=MAより、△MAB'は二等辺三角形、
よって、∠MAB'=∠MB'A。ところが、∠B'MBは△MAB'の外角なので、
∠B'MB=∠MAB'+∠MB'A
よって、
∠MAB'=∠MB'A=∠B'MC=∠BMC(=55°)
と分かります。従って、∠MAB'=∠BMCより、辺ABとMCは平行となり、
四角形AMNB'は平行四辺形となります。
よって、
B'N=AM ・・・ (2)
が示されます。(1)、(2)より、△B'NCと△AMCは、
B'C=BC、B'N=AM、および∠B'NC=∠AMC(平行線の同位角)となり、
∠二辺と一角(鈍角)が等しいので合同となります。よって、
四角形ABCD=△AMD+△MBC=△B'NC+△MBCとなります。ところが、四角形B'MBNは四辺が等しいので菱形、
Pを菱形の中心とすると、△MBPと△B'NPは合同な直角三角形となります。従って、
四角形ABCD=△CB'B
となります。点B'から辺BCに下ろした垂線の足をHとすると、∠B'CB=15×2=30°より、
B'H=B'C×1/2=10×1/2=5cmよって、
四角形ABCD=△CB'B=1/2×BC×B'H=1/2×10×5=25cm2
と求まります。
解答例3
uchinyanさん、他
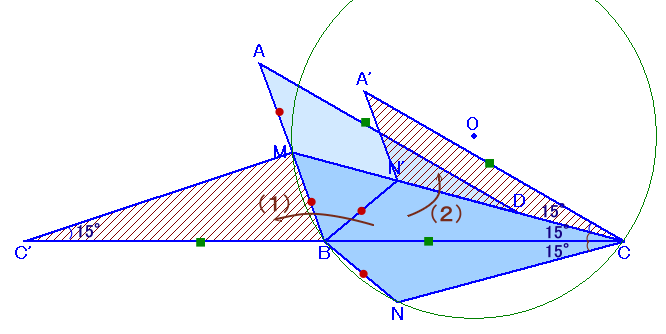
△AMCを回転移動し、点DがBに、点MがCと一致するようにしたものを△NBCとします。
すると、∠BMC+∠BNC=∠BMC+∠AMC=180°より、
点M、B、N、Cは一つの円周上(円Oとします)にあることが分かります。さて、辺BN=AM=辺MBより、弧BN=弧MBとなります。
従って、∠BNCと∠MCBは、長さが等しい弧に対する円周角なので等しくなります。
すなわち、
∠BNC=∠MCB=15°
となります。従って、辺BCを軸に△NBCを折りかえしたものを△N'BCとすると、
N'は辺MC上にくることが分かります。このあとは、
・△N'BCを△MBCの左側に移動すると解答例1と、
・辺N'Cを軸に折りかえすと解答例2と
同様にして面積を求めることが出来ます。
ここでは、uchinyanさんによる別解をご紹介しましょう。(この項、04.12.14追加)
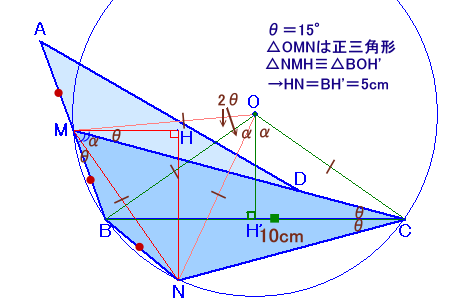
θ=∠MCB=∠NCB=15°、∠BMC=αとおきます。
点Mを通りBCと平行に引いた直線へNから下ろした垂線の足をHとし、
また円の中心OからBCに下ろした垂線の足をH'とします。
∠MOBは弧MBの中心角で、∠MCBは円周角だから、
∠MOB=∠MCB×2=2θ
同様に、
∠NOB=∠NCB×2=2θ従って、
∠MON=∠MOB+∠NOB=4θ=60°
よって、OM=ON(円の半径)より、△OMNは正三角形となります。
従って、MN=OB=OC(円の半径)となります。 ・・・ (1)次に、MHとBCは平行だから、
∠HMC=∠MCB=θ
そして、
∠BON=∠BCN=θ(弧BNの円周角)よって、
∠NMH=∠BMC−∠BMN+∠CMH=α−θ+θ=α
となります。また、∠BOCは弧BCの中心角で、∠BMCは円周角だから、
∠BOC=∠BMC×2=2α
そして、△OBCは二等辺三角形だから、
H'はBCの中点で、OH'は∠BOCの二等分線
よって、
∠BOH'=∠BOC×1/2=α ・・・ (2)
となります。(1)、(2)より、△NMHと△BOH'は合同な直角三角形とわかります。
従って、
NH=BH'=BC×1/2=5cmよって、
四角形ABCD=四角形MBNC=1/2×BC×NH=1/2×10×5=25cm2
と求まります。
解答例4
tomhさん、K.N.I.F.E.さん、ハラギャーテイさん、他
三角関数を使って解いてみましょう。
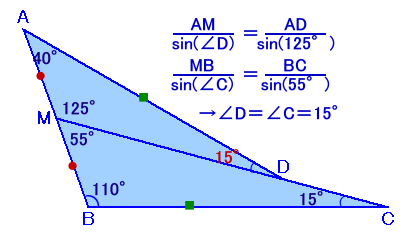
△AMDと△MBCについて、正弦定理より、
AM/sin(∠ADM)=AD/sin125°・・・ (1)
MB/sin(∠MCB)=BC/sin55°・・・ (2)ところが、
AM=MB、AD=BC=10cm、sin125°=sin(180°−55°)=sin55°
だから、(1)、(2)より、
sin(∠ADM)=sin(∠MCB) ・・・ (3)
となります。∠ADMと∠MCBは、いずれも鋭角なので、(3)より、
∠ADM=∠MCB=15°
を得ます。また、(2)より、
AM=MB=10×sin15°/sin55°従って、
△ADD=1/2×AD×AM×sin40°=1/2×10×10×sin15°/sin55°×sin40°
△MBC=1/2×BC×MB×sin110°=1/2×10×10×sin15°/sin55°×sin110°
よって、
四角形ABCD=△ADD+△MBC=50×sin15°/sin55°×(sin40°+sin110° ) ・・・(4)
となります。さて、三角関数の加法定理より、
sin(α+β)=sinα cosβ+cosα sinβ ・・・(5)
sin(α−β)=sinα cosβ−cosα sinβ ・・・(6)
(5)+(6)より、
sin(α+β)+sin(α−β)=2sinα cosβ ・・・(7)
を得ます。そこで、
α+β=110°、α−β=40°
を満たす
α=75°、β=35°
を(7)に代入して、
sin110°+sin40°=2×sin75°×cos35°=2×cos15°×sin55° ・・・(8)(4)、(8)より、
四角形ABCD=50×sin15°/sin55°×2×cos15°×sin55°
=50×2×sin15°×cos15°
=50×sin30°=50×1/2 =25cm2
と求まります。
(その他の解法)
CADを使用して図形を書いて求めた ・・・ kasamaさん、他
方程式を解いて求めた ・・・ ゴンともさん、他