第432問の解答
問題[ 推理]
|
|
|
|
|
|
算チャレ共和国では、次のような種類の硬貨が流通しています。
この国ではジュースは1本104円ですが、国民は上記の硬貨のうち(どのような組み合わせでもいいから)20種類を1枚ずつ所有していれば、必ず2枚の硬貨で(ぴったり)支払うことができるので、特に不便は感じていないそうです。 では、この国で流通している硬貨の中で、最大金額のもの(上の?に当てはまる数)として考えられるもののうち、最大のものを答えてください。 |
|
|
|
|
|
解答例1
あ〜く@ぴかぴかの(略さん、辻。さん、Taroさん、アヒーのおじさんさん、uchinyanさん、みかんさん、なかさん、スモークマンさん、N.Nishiさん、akiraさん、takaisaさん、トトロ@Nさん、エルクさん、arijuneさん、他
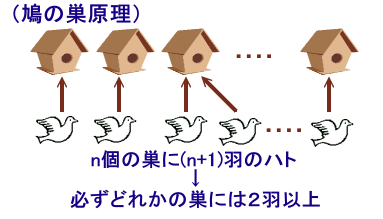
鳩の巣原理を用います。
(鳩の巣原理)
n個の巣に(n+1)個のハトが入れば、必ずどれかの巣には2羽以上
(証明)
どの巣にも1羽以下のハトしか入っていないと仮定すると、ハト合計数≦nとなって矛盾する。
よって、どれかの巣には2羽以上入っていることになります。さて、鳩の巣原理を念頭において本問を考えてみましょう。
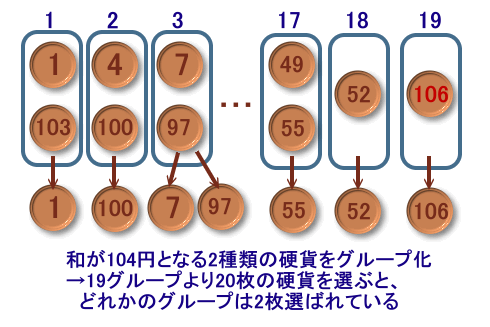
この国の硬貨のうち、和が104円となる2種類の 硬貨をペアにしてグループをつくっていきます。
ただし、104円の半分となる52円玉、および104円を超える額の硬貨は単独で1グループを作ることになります。(52−1)÷2+1=18なので、1円玉から52円玉までで18グループとなります。
55円玉から103円玉までは、これらのグループに入りますが、
106円玉は新しいグループ、すなわち19番目のグループとなります。1円玉から106円玉までの中から20種類の硬貨を選ぶと、鳩の巣原理により、
必ずどれかのグループから2枚の硬貨が選ばれることになります。
従って、この2枚の硬貨で104円のジュースを買うことが出来ます。ところが、109円玉を加えると20グループになるので、各グループより1枚ずつ20種類の硬貨を選ぶことにより、どうやっても2枚の硬貨で104円となることはありません。
従って、 題意を満たすような最大の硬貨は106円玉と求まります。
答: 106円玉
以上