第433問の解答
問題[推理、整数の性質]
|
|
|
|
|
|
ある整数を見て、14人の人が次々にコメントを残しました。
この14人の中に2人だけ嘘つきが混じっていて、しかもその2人は続けてコメントしたそうです。 |
|
|
|
|
|
解答例1
長野 美光さん、トトロ@Nさん、アヒーのおじさんさん、あ〜く@ジュークさん、辻。さん、きょろ文さん、uchinyanさん、hiroさん、エルクさん、小学名探偵さん、N.Nishiさん、M.Hossieさん、他
題意の整数をxとすると、次の補題が成り立つことに注目します。
(補題1)2〜15のある整数n、mについて、mがnの倍数なら、nはxの倍数である。
m=n×kと表すことが出来ます。従って、もしmがxの倍数でないとするとnがxの倍数であることと矛盾します。
(補題2)2〜15のある整数n、mについて、xがnおよびmの倍数ならば、xはn×mの倍数でもある。
こちらは明らかですね。
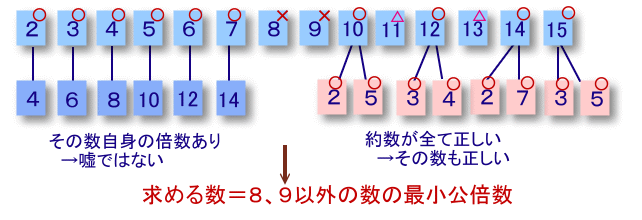
さて、2、3、4、5、6、7については、それぞれ2倍の4、6、8、10、12、14が2〜14に含まれるので補題1からxの倍数となり、嘘ではありません。
また、10=2×5、12=3×4、14=2×7、15=3×5と表されるので、これらは全てxの倍数。
よって、嘘の可能性が残るのは、8、9、11、13の4個となりますが、連続しているのは8と9の組み合わせのみです。
よって、xは8、9以外のすべての数の倍数で最小のものとなりますので、これらの最小公倍数ということになります。
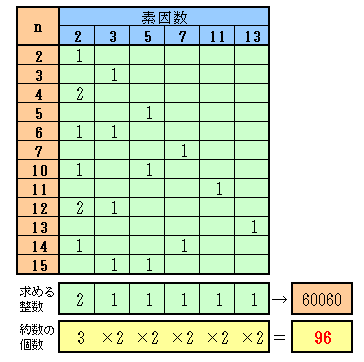
従って、各数を素因数分解し、各素因数のべき数の最大値を求めることでみると、上表より、
x=22×31×51×71×111×131=60060
と求まります。xの約数の個数は、各素因数のべき数+1の積で表されるので、
(2+1)×(1+1)×(1+1)×(1+1)×(1+1)=96個
と求まります。答: 96個
以上
解答例2
ゴンともさん、ハラギャーテイさん、DrKさん、姉小路さん、他
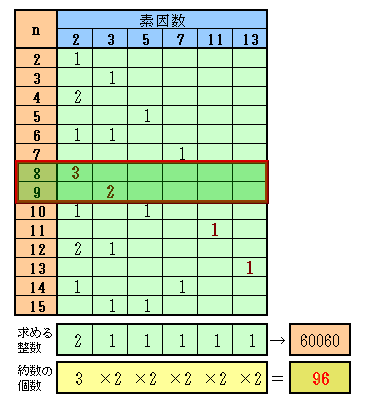
2〜14までを素因数分解すると下表のようになります。
もし、n=2k2×3k3×・・・×13k13×がxの倍数でないとすると、
どれかの素因数mについてxはmkmの倍数でないことになります。従って、このときのkmは他の数のmのべき数よりも必ず大きくないといけません。
もしそうでないと、その数の倍数でないことになるからです。このことから、素因数2のべき数が最大である8、素因数3のべき数が最大である9、および11と13が嘘の可能性ありということになります。
(その他の解法)
プログラムで求める ・・・ kasamaさん、Revinさん、 他