第436問の解答
問題[平面図形]
|
|
|
|
|
|
|
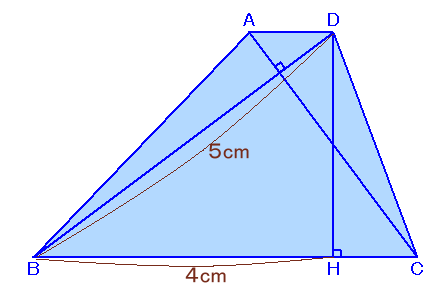 |
左図のような台形ABCDがあります。 いま、点Dから辺BCに垂線DHを下ろしたところ、BD=5cmとなりました。また、対角線BDと対角線ACは直角に交わっており、BHの長さは4cmでした。 このとき、台形ABCDの面積を求めてください。 |
|
|
|
|
|
|
解答例1
N.Nishiさん、M.Hossieさん、ゴンともさん、hiroさん、他
ACとBDの交点をPとします。
まず、DB=5cm、BH=4cmより、
△DBHは、辺の長さの比が3:4:5の直角三角形となります。すると、ADとBCは平行より、∠ADP=∠CDP(錯角)、
よって、△ADPと△CBPは、△DBHと相似な直角三角形となります。従って、
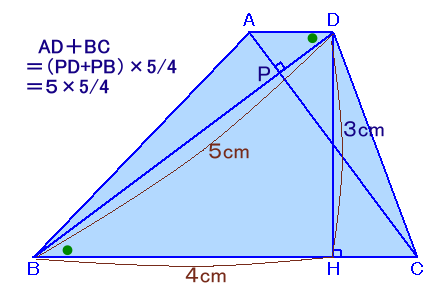
AD+BC=PD×5/4+PB×5/4
=(PD+PB)×5/4=5×5/4
=25/4cmよって、
台形ABCD=1/2×(AD+BC)×DH
=1/2×25/4×3=75/8cm2
と求まります。答: 75/8cm2
以上
解答例2
CRYING DOLPHINさん、arijuneさん、uchinyanさん、アヒーのおじさんさん、DrKさん、n厨さん、エルクさん、明大さん、他
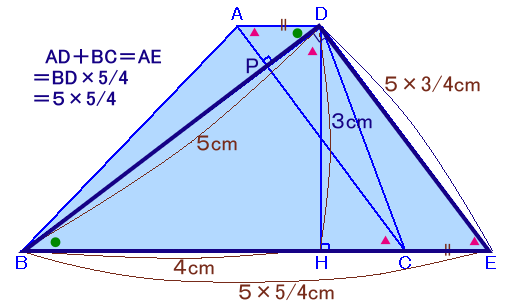
辺BCの延長線上に点Eを、CE=ADとなるように取ります。
(台形ABCDを180°回転し、DCで合わせる方法もこれに含めます)
すると、ADとCEは平行でAD=CEより、
四角形ACEDは平行四辺形となります。解答例1と同様にして、△ADPは、△DBHと相似な直角三角形となり、
∠ADP=∠DBH、∠DAP=∠BPHで、∠ADP+∠DAP=∠DBH+∠BPH=90°また、∠DECと∠DACは平行四辺形ACEDの相対する角だから等しい。
よって、∠DEB+∠DBE=∠ADP+∠DAP=90°従って、△EBDも△DBHと相似な直角三角形となります。
よって、
BE=BD×5/4=5×5/4=25/4cm、
DE=BD×3/4=5×3/4=15/4cm従って、
AD+BC=CE+BC=BE=25/4cm
以下、同様。あるいは、AD=CEより、△ADB=△DCEとなり、
平行四辺形ABCD=直角三角形EBD=1/2×BD×DEとして求める方法もあります。
解答例3
あ〜く@ジュークさん、uchinyanさん、他
辺DAの延長線上に点Eを、AE=CHとなるように取り 、EHとDBの交点をQとします。
すると、△EHCAは平行四辺形となるので、EHとACは平行、
よって、∠BQH=∠BPC=90°となります。よって、∠QHB=90°−∠QBH=∠BDH、
従って、∠EHD=90°−∠QHB=90°−∠BDH=∠DBH。 ・・・ (1)ADとBCは平行だから、∠EDH=∠DHB=90°、・・・ (2)
よって、△EHDは△DBHと相似な直角三角形となります。従って、ED=DH×3/4=3×3/4=9/4cm、
よって、AD+BC=AD+(BH+HC)=BH+(AD+EA)=4+9/4=25/4cm以下、同様。
解答例4
nobuさん、トトロ@Nさん、kazsyunさん、uchinyanさん、他
解答例1と同様にして、△ADPと△CBPは、△DBHと相似な直角三角形
従って、
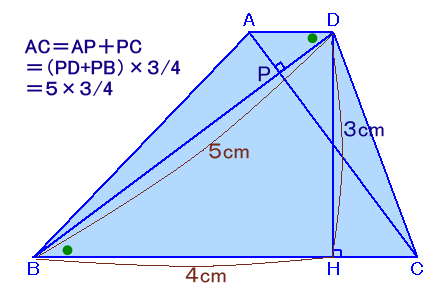
AC=AP+PC=PD×3/4+PB×3/4
=(PD+PB)×3/4=3×5/4
=15/4cmよって、
台形ABCD=△BAC+△DAC
=1/2×AC×PB+1/2×AC×PD
=1/2×AC×(PB+PD)1/2×AC×BD
=1/2×15/4×5
=75/8cm2
と求まります。
(その他の解法)
特別な場合を想定して求める ・・・ 姉小路さん、みかんさん、まるケンさん、きょろ文さん、なかさん、圭太さん、スモークマンさん、万打無さん、最近全然覗いてませんでしたさん、他
座標を用いて解く ・・・ UnderBirdさん、他
CADで描いて求める ・・・ kasamaさん、他