第４３７問の解答

問題［平面図形、整数の性質］

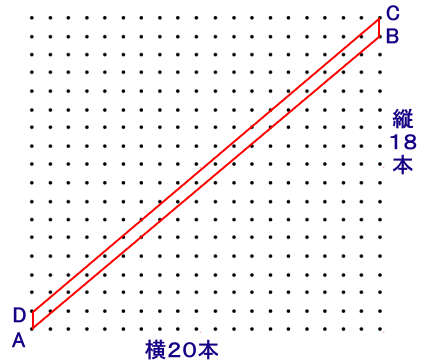左図は、ある板の上に１cm間隔で、縦１８本、横２０本の長方形になるようにクギを打ったところを表しています。

いま、この板の左下のクギＡとそのすぐ上のクギＤ、右上のクギＣとそのすぐ下のクギＢを選び、ＡＢ、ＣＤがそれぞれ一直線になるように輪ゴムをかけました。

輪ゴムの内側にあるクギを１本えらび、その１本とＡとＢを結んで三角形を作ります。このとき、できる三角形の面積は最も小さい場合で何cmでしょうか。

解答例１

Taroさん、N.Nishiさん、DrKさん、エルクさん、tomhさん、アヒーのおじさんさん、カエさん、y.kobayashiさん、経友会の進作さん、uchinyanさん、万打無さん、tapuさん、RDさん、arcさん、阪急大好き！さん、ゴンともさん、他

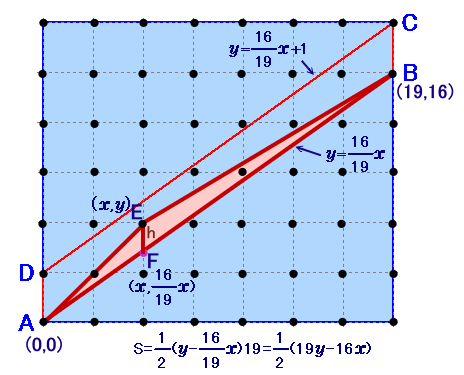
Aを原点とする座標で考えます。

A(0、0)、B(19、16)、C(19、17)、D(0、1)、
AB：y=16/19x、DC：y=16/19x＋１
と表せます。

平行四辺形ABCDの内部格子点E(x、y)に対し、
Eを通りy軸と平行な直線とABの交点をF、h＝EFとすると、F（x、16/19x)、
　△EAB＝△EAF＋△EFB＝1/2×ｈ×x＋1/2×ｈ×(19－x）＝1/2×ｈ×19

従って、△EABを最小にするには、ｈを最小にすればいいので、
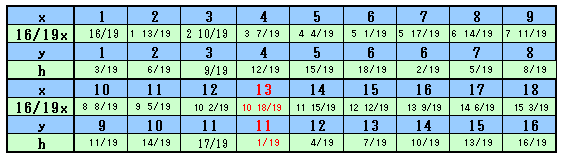
yは16/19xを切り上げた整数となります。

ｘ=1～18のとき、これらの値を求めると、ｘ＝１３のとき最小で、
　16/19x＝10 18/19、y＝１１、ｈ＝1/19
となります。

従って、
　△EABの最小値＝１/２×１/１９×１９＝１/２cm²　
と求まります。

答：１/２cm²

以上

解答例２

きょろ文さん、DrKさん、arijuneさん、ほげさん、M.Hossieさん、ｎ厨さん、さいと散さん、他

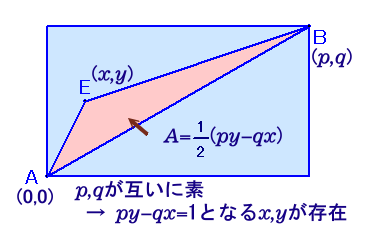
一般化して、B（p、q）(ただし、p、qは２以上の整数で、互いに素)として考えてみましょう。

解答例１と同様にしても求めることができますが、
ベクトルAE＝(x、y)、AB＝(ｐ、ｑ)に対して、よく知られたように、
　△EAB＝１/２×|py-qx|＝１/２×（py-qx）
と求まります。（EがABより上にあるので、py-qx＞０）

ｐ、ｑ、ｘ、ｙいずれも整数だから、py-qxも整数値となります。

ところが、ｐとｑが互いに素であることから、整数論の有名な性質より、
　py-qx＝１　・・・　（１）
を満たす整数解(ｘ₀、ｙ₀)が存在します。

このとき、
　py₀-qx₀＝１　・・・　（２）

（１）、（２）より、
　p(y-y₀)＝q(x-x₀)
ｐとｑが互いに素より、x-x₀はpの倍数。
よって、一般解x、yは、
　x＝kp＋x₀
　y＝kq＋y₀
と表すことができます。

さて、整数kを１ずつ増加・減少させると、xはpずつ増加・減少します。
よって、適当な整数kをとると、0≦ｘ＜pとなります。

もし、ｘ＝0とすると、y＝1/pとなりますが、p＞１より、yは整数でないので不適。
従って、0＜ｘ＜p。

このとき、
　qx＜y＝（qx＋１）/p＜qx＋１
となるので、点Ｅ（x、ｙ）は平行四辺形ＡＢＣＤの内部格子点となります。

よって、
△EABの最小値＝１/２×１＝１/２cm²　
と求まります。

（別解）

x_i＝0、１、・・、p－１に対し、qx_iをpで割った余りを、z_iとして定義します。
このとき、z_iは全て異なる値をとります。

なぜなら、もしz_i＝z_kとします。(ただし、0≦i＜k<q)
すると、qx_i-qx_kとなり、q(x_i-x_k)＝0。
q＞0より、x_i＝x_kとなり、矛盾。

z_iはqx_iをpで割った余りより、０≦z_i＜pで、しかもp個の異なる値を取ることから、
いずれかのiについて、z_i＝p-1となり、
qx_i＝kp＋(p-1)となるｋ
が存在します。

このとき、x=x_i_、y=(z_i＋1)/pとすると、
　ｙ＝(qx_i＋1)/p＝（k＋１）
従って、
　py-qx＝p(k+1)-{(k+1)p-1}＝１
となり、E（ｘ、ｙ）は、格子点で（１）式を満たす点となります。
以下、省略。

解答例３

呑さん、小学名探偵さん、那由他さん、他

ピックの定理を利用します。

解答２同様にＢ（p、q）としたとき、p、qが互いに素より、AB上には、A、B以外には格子点はありません。

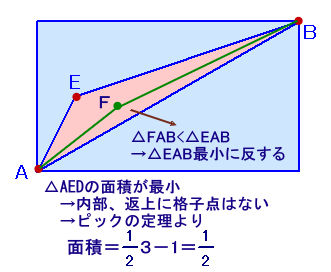
さて、△ＥＡＢが面積最小のとき、△ＥＡＢには内部および辺ＥＡ、ＥＢ上に格子点はありません。
なぜなら、もし△ＥＡＢの内部または辺上に格子点Ｆが存在するとしたとき、
△ＦＡＢ＜△ＥＡＢより、△ＥＡＢが面積最小に反します。

従って、内部点の個数Ｉ＝0、辺上の格子点数B＝頂点数＝３となることから、
ピックの定理より、最小値は、
　△ＥＡＢ＝１/２×３－１＝１/２
となります。

（その他の解法）

CAD等で図を描いて求める　・・・　kasamaさん、ハラギャーテイさん、他
　


	一般化して、B（p、q）(ただし、p、qは２以上の整数で、互いに素)として考えてみましょう。解答例１と同様にしても求めることができますが、ベクトルAE＝(x、y)、AB＝(ｐ、ｑ)に対して、よく知られたように、　△EAB＝１/２×\|py-qx\|＝１/２×（py-qx）と求まります。（EがABより上にあるので、py-qx＞０）ｐ、ｑ、ｘ、ｙいずれも整数だから、py-qxも整数値となります。ところが、ｐとｑが互いに素であることから、整数論の有名な性質より、　py-qx＝１　・・・　（１）を満たす整数解(ｘ₀、ｙ₀)が存在します。このとき、　py₀-qx₀＝１　・・・　（２）（１）、（２）より、　p(y-y₀)＝q(x-x₀) ｐとｑが互いに素より、x-x₀はpの倍数。よって、一般解x、yは、　x＝kp＋x₀ 　y＝kq＋y₀ と表すことができます。さて、整数kを１ずつ増加・減少させると、xはpずつ増加・減少します。よって、適当な整数kをとると、0≦ｘ＜pとなります。もし、ｘ＝0とすると、y＝1/pとなりますが、p＞１より、yは整数でないので不適。従って、0＜ｘ＜p。このとき、　qx＜y＝（qx＋１）/p＜qx＋１となるので、点Ｅ（x、ｙ）は平行四辺形ＡＢＣＤの内部格子点となります。よって、 △EABの最小値＝１/２×１＝１/２cm²　と求まります。（別解） x_i＝0、１、・・、p－１に対し、qx_iをpで割った余りを、z_iとして定義します。このとき、z_iは全て異なる値をとります。なぜなら、もしz_i＝z_kとします。(ただし、0≦i＜k<q) すると、qx_i-qx_kとなり、q(x_i-x_k)＝0。 q＞0より、x_i＝x_kとなり、矛盾。 z_iはqx_iをpで割った余りより、０≦z_i＜pで、しかもp個の異なる値を取ることから、いずれかのiについて、z_i＝p-1となり、 qx_i＝kp＋(p-1)となるｋが存在します。このとき、x=x_i_、y=(z_i＋1)/pとすると、　ｙ＝(qx_i＋1)/p＝（k＋１）従って、　py-qx＝p(k+1)-{(k+1)p-1}＝１となり、E（ｘ、ｙ）は、格子点で（１）式を満たす点となります。以下、省略。