第１３４問の解答

１．問題　［整数、不等式］

　ある学校で問題数が４問のテストが６年生全員に対して行われることになりました。
　その際、各問題の正解率（正解者の全体に占める割合）を百分率で発表することに決めました。
　ただし、参加者全員が正解した場合（正解率１００％）、および全員が不正解の場合（正解率０％）を除くと、正解率が割り切れない数値となることがあらかじめ分かっていました。
　そこで、小数点以下を四捨五入して整数で表すことに決めました。
　テストの結果、それぞれの問題の正解率は９９％、８８％、７７％、６６％と発表されました。
　また、全問正解の人が２２人いたということです。
　では、４問中３問が正解だった人は何人いたのでしょうか？

２．解答例１(たなかさん、トトロ＠Ｎさん、長野美光さん、DrKさん、他)

生徒数をn、各問題の正解者数と延べ正解者数をx1、x2、x3、x4、X、
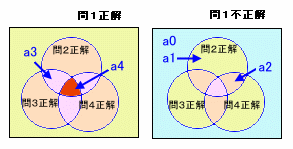
および全問不正解の人数をa0、1問正解をa1、・・・、4問正解をa4とします。

参考図1 参考図2

題意より、下記の式が成り立つ。
　　X=x1+x2+x3+x4　　　・・・（１）
　　X=a1+2a2+3a3+4a4　・・・（２）
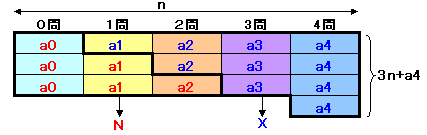
　　n=a0+a1+a2+a3+a4　・・・（３）

（３）×３−（２）より、
　　3a0+2a1+a2-a4=3n-X
よって、
　　N=3a0+2a1+a2=3n+a4-X=3n+22-X ・・・（４）

参考図3

また、
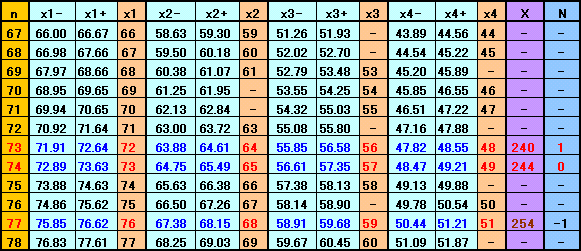
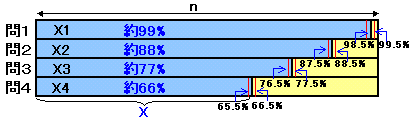
　　0.985n≦x1<0.995n、0.875n≦x2<0.885n、
　　0.765n≦x3<0.775n、0.655n≦x4<0.665n　・・・（５）
（0.985+0.875+0.765+0.655)n≦X=x1+x2+x3+x4
　　　　＜(0.995+0.885+0.775+0.665)n
よって、3.28n≦X<3.32n　　・・・（６）

N≧0だから、（４）より、3n-X+22≧0、3n+22≧X≧3.28n（∵（６））
0.28n≦22、よってn≦22/0.28≒78.57

また、0.985n≦x1≦n-1より、1≦0.015n、n≧1/0.015≒66.67

よって、67≦n≦78。

参考図4

この範囲のｎで（５）を満たす整数x1,x2,x3,x4が存在するのは、
n=73,74,77の３通り。

0,n以外のどんな正解者数のときでも正解率の百分率は割り切れないことから、ｎは２と５の倍数ではないので、n=74は不適。

n=77のとき、x1=76、x2=68、x3=59、x4=51となるので、X=254、
（４）よりN=3×77-254+22=-1となり不適。

n=73のとき、x1=72、x2=64、x3=56、x4=48となるので、X=240、
（４）よりN=3×73-240+22=1、
すなわち3a0+2a1+a2=1でa0、a1、a2≧0だからa0=a1=0、a2=1。
よって、a3=n-(a0+a1+a2+a4)=73-(1+22)=50となる。

よって、４問中３問正解者は、a3=５０人となります。

答：５０人

以上