第１３５問の解答

---

１．問題　［平面図形］

左図は、直径が１６ｃｍの円を４５度で交わる２本の線で区切って色分けした図です。 　ピンク色に塗ってある部分の面積は何ｃｍ2でしょうか。 円周率を３．１４として求めて下さい。

---

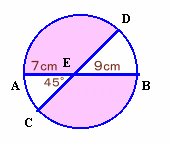２．解答例１(ヒデー王子さん、長野美光さん、中村明海さん、杉本未来さん、他)

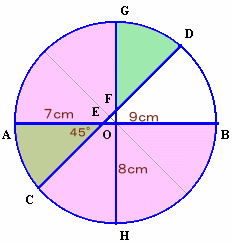
下図のように円の中心をOとし、Oを通る垂直線と円との交点をＧ、Ｈとします。

Oを通り、ＣＤと垂直な直線を軸にして対象なことから、ＦＧＤの面積はＡＥＣの面積に等しい。

よって求める面積は、３/４円ＯＧＢの面積から直角２等辺三角形ＯＥＨの面積を除いた
　３．１４×８²×３/４−１/２×１²＝１５０．７２−０．５＝１５０．２２ｃｍ²
となる。
　

答：１５０．２２ｃｍ²

以上

---

３．解答例２(あやのりんさん、ハラギャーテイさん、大沢さん、大岡敏幸さん、DrKさん、他)

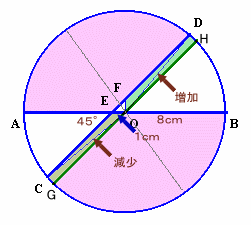
ＣＤを円の中心Ｏを通るＧＨまで平行にずらします。

対称性から元の図形より増加する部分ＯＦＤＨと減少するのＯＥＣＧ面積は等しいので、求める面積は、１３５度の扇形が２個から２等辺三角形ＯＥＦを除いたものとなる。
よって、求める面積＝３．１４×８²×１３５／３６０×２−１/２×１²＝１５０．２２ｃｍ²

---