第１３６問の解答

１．問題　［平面図形、規則性］

問題図

　半径７ｃｍの円を左図のように２ｃｍずつ平行にずらして描きます。
このときにできる領域の個数を数えると、
　・円が１個の場合は領域も１個
　・円が２個の場合は領域が３個
　・円が３個の場合は領域が７個
・・・と変化します。
　では、円を１０個描いたときの領域の個数は、いくつでしょう？

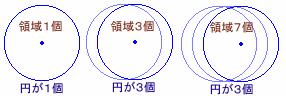２．解答例１(ありっちさん、杉本未来さん、Hamayanさん、マツダさん、パリンさん、シイサンさん、ＫＩＮさん、下田康夫さん、萬田銀次郎さん、okaokaさん、こいずみさん、大沢幸一さん、うっしーさん、他多数)

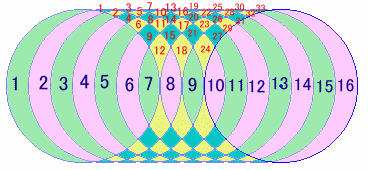
実際に作図してみると、下図のようになります。

参考図1

真ん中に領域が１６個、上下に３３個ずつ、
よって、合計＝１６＋３３×２＝８２個になります。

答：８２個

以上

３．解答例２(ταροさん、トトロ＠Ｎさん、吉川マサルさん、長野美光さん、中村明海さん、有無相生さん、他)

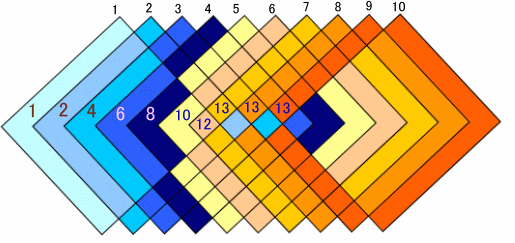
n番目の円を描いたときに、領域がいくつ増えるかを考えてみましょう。
円だと領域が分かりにくいので、下図では正方形で代用しました。

参考図2


7個目の円までは、それまでに書かれたすべての円と交わるので 境界が2,4,6,8,10,12と増えますが、8個目からは1つの円と接して 他の6個の円と交わるので境界が13ずつ増えます。 

したがって、円が１０個のとき領域は、
　1+2+4+6+8+10+12+13+13+13=82個
になります。