第138問の解答
1.問題 [整数、場合の数]
|
大きさが1より小さく、分母が1001である全ての既約分数の合計は、 |
2.解答例1(ταροさん、C-Dさん、トトロ@Nさん、長野美光さん、ありっちさん、香川仁志さん、有無相生さん、大岡敏幸さん、他多数)
分子について考えることにします。
1001=7・11・13なので、既約分数の分子は7、11、13とそれぞれ互いに素となります。
互いに素な整数を数えるのは面倒なので、替わりに7、11、13のいずれかの倍数となる整数を数えることにします。
1から1001までの整数の中には、7・11・13=1001の倍数はありません。
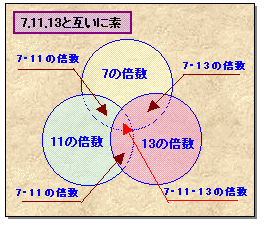
上図から、7の倍数と11の倍数と13の倍数を加えると、7・11の倍数、7・13の倍数、11・13の倍数を重複して数えていることになります。従って、7、11、13のいずれかの倍数の和=
7の倍数の和+11の倍数の和+13の倍数の和
−(7・11の倍数の和+7・13の倍数の和+11・13の倍数の和)7の倍数の和=7・(1001/7)・(1001/7−1)/2=71071
11の倍数の和=11・(1001/11)・(1001/11−1)/2=45045
13の倍数の和=13・(1001/13)・(1001/13−1)/2=38038
7・11の倍数の和=7・11・(1001/7・11)・(1001/7・11−1)/2=6006
7・13の倍数の和=7・13・(1001/7・13)・(1001/7・13−1)/2=5005
11・13の倍数の和=11・13・(1001/11・13)・(1001/11・13−1)/2
=3003よって、7、11、13のいずれかの倍数の和
=71071+45045+38083−(6006+5005+3003)
=1401401から1000までの整数の和=1000・1001/2=500500だから
互いに素な整数の和=500500−140140=360360よって、規約分数の和=360360/1001=360となります。
答:360
以上
3.解答例2(ヒデー王子さん、清川育男さん、柚奇神太郎さん、他多数)
解答例1で、n=1001、p=7、q=11、r=13とおきます。
今度は、1からn=1001までの整数で考えます。
mの倍数の個数をN(m)、倍数の和をS(m)とします。N(m)=n/m、S(m)=m・(n/m)・(n/m+1)/2となります。
従って、p、q、rのいずれかの倍数の個数
=N(p)+N(q)+N(r)−(N(pq)+N(pr)+N(qr))+N(pqr)
=qr+pr+pq-(r+q+p)+1
よって、互いに素な整数の個数
=pqr-(pq+qr+rp)+(p+q+r)-1
=(p-1)(q-1)(r-1) ・・・(1)
となります。また、p、q、rのいずれかの倍数の和
=S(p)+S(q)+S(r)−(S(pq)+S(pr)+S(qr))+S(pqr)
=n{(qr+1)/2+(pr+1)/2+(pq+1)/2}-n{(r+1)/2+(q+1)/2+(p+1)/2}+n
=n{qr+pr+pq-(r+q+p)+1}/2
よって、互いに素な整数の和
=n(pqr+1)/2-n{(pq+qr+rp)+(p+q+r)-1}/2
=n(p-1)(q-1)(r-1)/2
従って、規約分数の和
={n(p-1)(q-1)(r-1)/2}/n
=(p-1)(q-1)(r-1)/2
=6・10・12/2
=360 となります。
4.解答例3(noetherさん、他)
(1)は、一般にオイラー関数と呼ばれ、
自然数nでnと互いに素な自然数の個数をφ(n)、
n=paqbrc・・・と素数巾の積に分解されるとき、
φ(n)=n(1-1/p)(1-1/q)(1-1/r)・・・
と表されます。
このオイラー関数を適用すれば、
φ(pqr)=pqr(1-1/p)(1-1/q)(1-1/r)
=(p-1)(q-1)(r-1)=720
と求まります。ここで、1からn以下の整数mがnと互いに素ならn-mとnも互いに素であることに着目します。
なぜなら、もしmとnが互いに素で、n-mとnが公約数sを持つとしたら、
n-m=st、n=suと表せます。
すると、m=n-st=s(u-t)となり、mとnが共通な公約数sを持つことになり、矛盾。逆も同様。
よって、N=互いに素な整数の個数、S=互いに素な整数の和とすると、
S=s1+s2+・・+sN(s1+sN=s2+sN-2=・・)と表せます。
2S=(s1+s2+・・+sN)+(sN+sN-1+・・+s1)
=(s1+sN)+(s2+sN-2)+・・(sN+s1)
=nN
よって、S=nN/2となります。
これから、規約分数の和=S/n=N/2=360と求まります。