第１３９問の解答

１．問題　［平面図形］

問題図

　３つの合同な扇形ＯＡＤ、ＰＢＤ、ＱＣＤを、
Ｐが孤ＡＤ上に、Ｑが孤ＢＤ上にくるように重ねました。
　こうしてＡとＣを結んだところ、ＡＣとＰＤの交わる角度（●印）が１０８度になりました。
　では、この扇形の中心角（▲印）は何度になるでしょうか？

（注意）図は正確とは限りません。

　

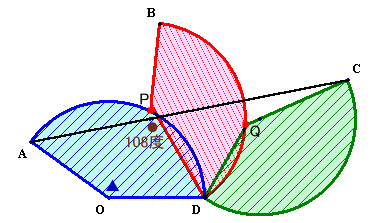２．解答例１(ありっちさん、香川仁志さん、YokoyaMacさん、トトロ＠Ｎさん、有無相生さん、noetherさん、中村明海さん、げんたさん、数楽者さん、とりやまじゅんさん、大沢幸一さん、他多数)

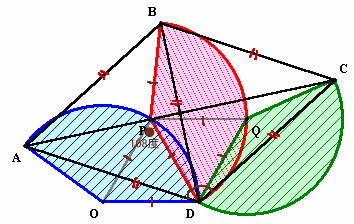
ＯＰを結び、三角形ＯＰＤを考えます。

参考図1

ＯＰ、ＯＤ、ＰＤは、いずれも扇形の半径だから全て等しい。
よって、△ＯＰＤは正三角形となり、∠ＰＯＤ＝６０度。
すなわち、扇形ＢＱＤは、扇形ＡＯＤを６０度回転させたものになります。

従って、ＡＤ＝ＢＤ、∠ＡＤＢ＝６０度。
よって、△ＡＢＤも正三角形となり、ＡＢ＝ＡＤ、∠ＡＢＤ＝∠ＢＤＡ＝６０度。

同様に、△ＢＣＤも正三角形となり、ＢＣ＝ＣＤ、∠ＣＢＤ＝∠ＣＤＢ＝６０度。

よって、四角形ＡＢＣＤは、菱形となり、ＡＣとＢＤは、互いに相手の垂直二等分線になります。（補題参照）

また、ＰＢ＝ＰＤなので、ＰもＢＤの垂直二等分線（ＡＣ）上にあることとなります。

すると、ＣＰＤ＝１８０−１０８＝７２度。
扇形の中心角ＢＰＤ＝７２×２＝１４４度となります。

答：５４通り

以上

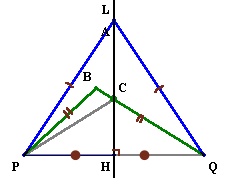
（補題）点Ｐ、Ｑから等距離にある点の集合は、ＰＱの垂直二等分線Ｌと一致する。

ＰＱの中点をＨとする。

参考図2

直線Ｌ上の任意の点Ａについて考える。
△ＡＨＰと△ＡＨＱは、
　ＰＨ＝ＱＨ、ＡＨは共通、∠ＡＨＰ＝∠ＡＨＱ＝直角、
より合同。よって、ＡＰ＝ＡＱ。　・・・（１）

逆に、ＢＰ＝ＢＱとなる任意の点Ｂについて考える。
もし、ＢがＬ上にはなく、Ｌに関してＢとＰが同じ側にあると仮定する。
ＢＱとＬの交点をＣとすると、（１）より、ＣＰ＝ＣＱ。
仮定から、ＢＰ＝ＢＱ＝ＢＣ＋ＣＱ＝ＢＣ＋ＣＰ。
これは、△ＢＣＰの二辺の和が、もう一つの一辺と等しいことになるので矛盾。
Ｌに関してＢとＱが同じ側にあると仮定しても同様。
よって、ＢはＬ上にあることになる。　・・・（２）

（１）、（２）より、補題が成り立つことが示された。

３．解答例２(mhayashiさん、他)

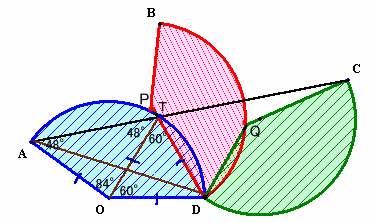
ＡＣとＰＤの交点をＴとし、ＴＯ、ＡＤをそれぞれ結びます。。

参考図3

解答例１と同様にして、△ＴＯＤは正三角形、∠ＯＴＤ＝∠ＴＯＤ＝６０度となります。
∠ＡＴＯ＝∠ＡＴＤ−∠ＯＴＤ＝１０８−６０＝４８度。

ＯＡ＝ＯＴより、△ＯＡＴは二等辺三角形、∠ＴＡＯ＝∠ＡＴＯ＝４８度。
よって、∠ＡＯＴ＝１８０−４８×２＝８４度。

従って、∠ＡＯＤ＝∠ＡＯＴ＋∠ＴＯＤ＝８４＋６０＝１４４度。