第１４１問の解答

１．問題　［場合の数］

問題図
黒色のボールが１０個、赤色のボールが５個と、３×５のマス目に区切られた透明なアクリル製の箱があります。
１５個のボールを、この１５マスに１個ずつ入れるとき、上から見た模様が点対称になるようなボールの入れ方は何通りあるでしょうか？
ただし、箱を裏返して反対側から見たときに同じ模様に見える入れ方は同一の入れ方として、１通りと数えます。

２．解答例１
(わかさひ君すーぱーさん、トトロ＠Ｎさん、ταροさん、ありっちさん、たなかさん、航介さん、DrKさん、他多数)

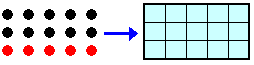
赤のボールが点対称になっていれば、残りは全て黒のボールですから全体でもそうです。従って、赤のボールのみを考えれば十分です。
また、赤いボールの個数は奇数なので、１個は必ず真ん中にあります。

参考図1

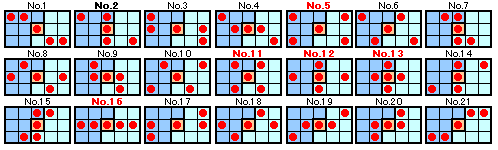
従って、上図のように真ん中を除く１４個のマス目を７個ずつに分けると、赤いボールの置き方は７個から２個を選ぶ選び方7C2=21通りになります。

参考図2

このうち、箱を裏返して反対側から見たときに同じ模様に見える入れ方を１通りと見なすため、始めから線対称の５通り（No.5、No.11、No.12、No.13、No.16）
を除く２１−５＝１６通りは、実際にはこの半分の８通りになります。

よって、求める場合の数は、５＋８＝１３通りになります。

答：１３通り

以上