第１４２問の解答

---

１．問題　［整数の性質］

日本に住んでいるＴＯＲＡさんは、海外に住む妹のＳＡＷＡＫＯさんに、久しぶりに電話を掛けてみました。 　ＴＯＲＡ：「今そっちの時間で何時やねん？」 　ＳＡＷＡＫＯ：「ちょうど●時だけど。」 　ＴＯＲＡ：「それやったら、こっちのちょうど３倍の数字やん。」 それから何時間かして、今度はＳＡＷＡＫＯさんからＴＯＲＡさんに電話が掛かってきました。 　ＳＡＷＡＫＯ：「今そっちの時間で何時なの？」 　ＴＯＲＡ：「そっちの時間のちょうど３倍だよ。」 さて、今の時間、ＴＯＲＡさんの住む日本では何時なのでしょうか？ （注）二人は、時刻を１時〜２４時の整数の数字で言い表しています。 　　　考えられる全ての数字を答えて下さい。

---

２．解答例１(ταροさん、ありっちさん、他多数)

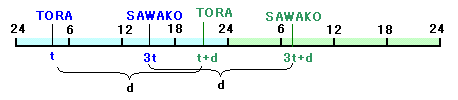
最初の時点で、ＴＯＲＡさんの住む日本の時刻をｔとすると、ＳＡＷＡＫＯさんの住む国の時刻は、３ｔになります。

これから、ｄ時間経過して今になったとすると、ＳＡＷＡＫＯさんの国では、翌日になっているはずで、、
　　３（３ｔ＋ｄ−２４）＝ｔ＋ｄ
よって、
　　４ｔ＋ｄ＝３６　　・・・　（１）

（１）より、ｔは、１≦ｔ≦２４の整数なので、ｄは４の倍数となります。
題意より、０＜ｄ＜２４と考えられるので、
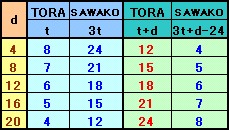
　　ｄ＝４、８、１２、１６、２０
このとき、
　　ｔ＝８、７、６、５、４
および、
　ｔ＋ｄ＝１２、１５、１８、２１、２４
となります。

答：１２、１５、１８、２１、２４時

以上

---

３．解答例２(萬田銀次郎さん、トトロ＠Ｎさん、数楽者さん、DrKさん、他)

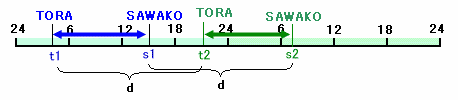
最初の時点で、ＴＯＲＡさん、ＳＡＷＡＫＯさんの住む国でのの時刻をｔ1、ｓ１、次の時点では、ｔ２、ｓ２とします。

　　ｓ１−ｔ１＝ｔ１×３−ｔ１＝ｔ１×２　・・・　（２）
　　ｔ２−ｓ２＝ｓ１×３−ｓ１＝ｓ１×２　・・・　（３）
　　ｓ２＋２４−ｔ２＝ｔ１×２
　　ｔ２−ｓ２＝２４−ｔ１×２　・・・　（４）
（２）、（４）より、
　　　　（ｓ１−ｔ１）＋（ｔ２−ｓ２）＝２４
ＴＯＲＡさんとＳＡＷＡＫＯさんの時間差（ｓ１−ｔ１）および（ｔ２−ｓ２）は、ともに２の倍数で和が２４となります。

（２）より、
　　ｔ１＝（ｓ１−ｔ１）／２
　　ｓ１＝ｔ１×３≦２４より、ｔ１≦８、
よって、
　　ｓ１−ｔ１＝ｔ１×２≦１６、８≦ｔ２−ｓ２。

（３）より、
　　ｓ２＝（ｔ２−ｓ２）／２
　　ｔ２＝ｓ２×３≦２４より、ｓ２≦８、
よって、
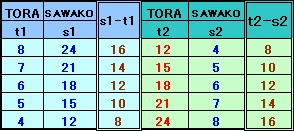
　　ｔ２−ｓ２＝ｓ２×２≦１６、８≦ｓ１−ｔ１。

以上から、８≦（ｓ１−ｔ１）、（ｔ２−ｓ２）≦１６となり、次のように求まります。

よって、ｔ２＝１２、１５、１８、２１、２４となります。

---