第１４４問の解答

---

１．問題　［規則性］

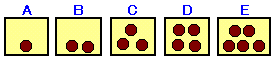
Ａ〜Ｅの５つの箱に、碁石がそれぞれ１〜５個のせてあります。 ２人でこの箱からかわりばんこに碁石を取っていって、最後に碁石を全部取り尽くした方が勝ち、というゲームをします。 ただし取り方には、 　・一度に同じ箱から複数の碁石をとっても良いが、別の箱から取ることはできない というルールがあります。 さて、先手側の立場にたっと時、最初にどのように取れば勝ちにつながるでしょうか？ 次の中から正しい方法を３つ選んでください。 ただし、２手目以降もお互いが最善の手をつくすものとします。 （Ａ−１） 　 　 （Ｂ−１） （Ｂ−２） 　 （Ｃ−１） （Ｃ−２） （Ｃ−３） 　　 　　 （Ｄ−１） （Ｄ−２） （Ｄ−３） （Ｄ−４） （Ｅ−１） （Ｅ−２） （Ｅ−３） （Ｅ−４） （Ｅ−５） （注）（Ｃ−２）とは、Ｃの箱から碁石を２個取ることを表すことにします。

---

２．解答例１(清川育男さん、LIONさん、C-Dさん、okaokaさん、有無相生さん、他多数)

まず、箱が２つの場合を考えてみましょう。
先手番のとき、箱の中の碁石が（Ｎ、Ｍ）（ただし、Ｎ＜Ｍ）であれば、Ｍ個の碁石をＮ個に減らし、（Ｎ、Ｎ）型にするようにすれば、
　・先手番では、必ず（Ｎ、Ｍ）型
　・後手番では、必ず（Ｎ、Ｎ）型
になる。
碁石の数は次第に減っていくので、最後は後手番で（０、０）となり、先手勝ちとなる。

すなわち、先手は、（Ｎ、Ｎ）となるようにできれば、先手必勝型である。

箱が３個の時、先手は（１、２、３）または（１、４、５）にできれば必勝型である。
（１、２、３）のとき、
　・後手（０、２、３）→先手（０、２、２）
　・後手（１、１、３）→先手（１、１、０）
　・後手（１、０、３）→先手（１、０、１）
　・後手（１、２、２）→先手（０、２、２）
　・後手（１、２、１）→先手（１、０、１）
　・後手（１、２、０）→先手（１、１、０）
と、後手がどのような手をとっても、先手は（Ｎ、Ｎ）型にできるので、先手必勝。
（１、４、５）のとき、
　・後手（０、４、５）→先手（０、４、４）
　・後手（１、３、５）→先手（１、３、２）
　・後手（１、２、５）→先手（１、２、３）
　・後手（１、１、５）→先手（１、１、０）
　・後手（１、４、４）→先手（０、４、４）
　・後手（１、４、３）→先手（１、２、３）
　・後手（１、４、２）→先手（１、３、２）
　・後手（１、４、１）→先手（１、０、１）
　・後手（１、４、０）→先手（１、１、０）
と、後手がどのような手をとっても、先手は（Ｎ、Ｎ）型または（１、２、３）の必勝型にできるので、先手必勝。

さらに、
　・箱が４個のときに（Ｎ、Ｎ、Ｍ、Ｍ）、
　・箱が５個のときに（Ｎ、Ｎ、１、２、３）または、（Ｎ、Ｎ、１、４、５）
にできれば、先手必勝型の組み合わせなので、やはり先手必勝型。

さて、本問の場合、
　（Ａ−１）→（２、３、４、５）
　（Ｃ−１）→（１、２、２、４、５）
　（Ｅ−１）→（１、２、３、４、４）
の３つのケースが先手必勝になります。

このうち、
　（Ｃ−１）→（１、２、２、４、５）は、（２、２）と（１、４、５）の組み合わせ、
　（Ｅ−１）→（１、２、３、４、４）は、（４、４）と（１、２、３）の組み合わせ、
になるので、先手必勝。

（Ａ−１）→（２、３、４、５）の場合は、
　・後手（１、３、４、５）→先手（１、０、４、５）
　・後手（０、３、４、５）→先手（０、１、４、５）
　・後手（２、２、４、５）→先手（２、２、４、４）
　・後手（２、１、４、５）→先手（０、１、４、５）
　・後手（２、０、４、５）→先手（１、０、４、５）
　・後手（２、３、３、５）→先手（２、３、３、２）
　・後手（２、３、２、５）→先手（２、３、２、３）
　・後手（２、３、１、５）→先手（２、３、１、０）
　・後手（２、３、０、５）→先手（２、３、０、１）
　・後手（２、３、４、４）→先手（２、２、４、４）
　・後手（２、３、４、３）→先手（２、３、２、３）
　・後手（２、３、４、２）→先手（２、３、３、２）
　・後手（２、３、４、１）→先手（２、３、０、１）
　・後手（２、３、４、０）→先手（２、３、１、０）
となり、後手がどのような手を取っても、先手は必勝型に持ち込める。

これ以外の手を先手が取った場合、
　・先手（Ｂ−１）→（１、１、３、４、５）の場合は、後手（１、１、１、４、５）
　・先手（Ｂ−２）→（１、０、３、４、５）の場合は、後手（１、０、０、４、５）
　・先手（Ｃ−２）→（１、２、１、４、５）の場合は、後手（１、１、１、４、５）
　・先手（Ｃ−３）→（１、２、０、４、５）の場合は、後手（１、０、０、４、５）
　・先手（Ｄ−１）→（１、２、３、３、５）の場合は、後手（１、２、３、３、３）
　・先手（Ｄ−２）→（１、２、３、２、５）の場合は、後手（１、２、３、２、２）
　・先手（Ｄ−３）→（１、２、３、１、５）の場合は、後手（１、２、３、１、１）
　・先手（Ｄ−４）→（１、２、３、０、５）の場合は、後手（１、２、３、０、０）
　・先手（Ｅ−２）→（１、２、３、４、３）の場合は、後手（１、２、３、３、３）
　・先手（Ｅ−３）→（１、２、３、４、２）の場合は、後手（１、２、３、２、２）
　・先手（Ｅ−４）→（１、２、３、４、１）の場合は、後手（１、２、３、１、１）
　・先手（Ｅ−５）→（１、２、３、４、０）の場合は、後手（１、２、３、０、０）
とすれば、後手が必勝型に持ち込むことができますので、解は上記３ケースしかありません。

答：（Ａ−１）、（Ｃ−１）、（Ｅ−１）

以上

---

３．解答例２(中村明海さん、高橋道広さん、他)

この問題は、有名な３山くずしと呼ばれるゲームで、２進数表示で考えると簡単に先手必勝型が分かります。

初期状態（1、2、3、4、5）は、それぞれの個数を2進数表示し、排他論理和（繰上りのない２進数の足し算、ニム和ともいいます）を計算すると 
　　1＝001
　　2＝010
　　3＝011　・・・・　（１）
　　4＝100
　+)5＝101
　　１＝00１
１になります。
先手は、ここから、ニム和が０になるような手を作ることが出来れば、必勝型になります。

ちなみに、解答例１で出てきた必勝型（Ｎ、Ｎ）、（１、２、３）、（１、４、５）は、いずれもニム和は０です。

（１）の計算でニム和が０になるようにするには、１の位が１のものを０にすればいいので、１から５では奇数の１、３、５のいずれかになります。

　

すなわち、（Ａ−１）、（C−１）、（E−１）の３ケースが先手必勝型です。

（Ａ−１） 　　 0＝000 　　 2＝010 　　 3＝011 　　 4＝100 　+) 5＝101 　　0＝000

（Ｃ−１） 　　 1＝001 　　 2＝010 　　2＝010 　　 4＝100 　+) 5＝101 　　0＝000

（Ｅ−１） 　　 1＝001 　　 2＝010 　　 3＝011 　　 4＝100 　+)4＝100 　　0＝000

　

なお、（Ａ−１）〜（Ｅ−５）についてニム和を計算すると下記のようになります。

（Ａ−１） 　　 0＝000 　　 2＝010 　　 3＝011 　　 4＝100 　+) 5＝101 　　0＝000
（Ｂ−１） 　　 1＝001 　　1＝001 　　 3＝011 　　 4＝100 　+) 5＝101 　　2＝010	（Ｂ−２） 　　 1＝001 　　0＝000 　　 3＝011 　　 4＝100 　+) 5＝101 　　3＝011
（Ｃ−１） 　　 1＝001 　　 2＝010 　　2＝010 　　 4＝100 　+) 5＝101 　　0＝000	（Ｃ−２） 　　 1＝001 　　 2＝010 　　1＝001 　　 4＝100 　+) 5＝101 　　3＝011	（Ｃ−３） 　　 1＝001 　　 2＝010 　　0＝000 　　 4＝100 　+) 5＝101 　　2＝010
（Ｄ−１） 　　 1＝001 　　 2＝010 　　 3＝011 　　3＝011 　+)5＝101 　　6＝110	（Ｄ−２） 　　 1＝001 　　 2＝010 　　 3＝011 　　2＝010 　+) 5＝101 　　7＝111	（Ｄ−３） 　　 1＝001 　　 2＝010 　　 3＝011 　　1＝001 　+) 5＝101 　　4＝100	（Ｄ−４） 　　 1＝001 　　 2＝010 　　 3＝011 　　0＝000 　+) 5＝101 　　5＝101
（Ｅ−１） 　　 1＝001 　　 2＝010 　　 3＝011 　　 4＝100 　+)4＝100 　　0＝000	（Ｅ−２） 　　 1＝001 　　 2＝010 　　 3＝011 　　 4＝100 　+)3＝011 　　7＝111	（Ｅ−３） 　　 1＝001 　　 2＝010 　　 3＝011 　　 4＝100  　+)2＝010 　　6＝110	（Ｅ−４） 　　 1＝001 　　 2＝010 　　 3＝011 　　 4＝100 　+)1＝001 　　5＝101	（Ｅ−５） 　　 1＝001 　　 2＝010 　　 3＝011 　　 4＝100 　+)0＝000 　　4＝100

従って、（Ａ−１）、（Ｃ−１）、（Ｅ−１）以外ではニム和が０にならないことがわかります。

（参考）ニム和０が先手必勝型の証明 箱Ａ、Ｂ、Ｃ、Ｄ、Ｅにある碁石の個数をａ、ｂ、ｃ、ｄ、ｅとします。 先手番で、ｓ＝ａ＋ｂ＋ｃ＋ｄ＋ｅ（ニム和：以下同様）が０でないとします。 例えば本問では、ｓ＝１です。 ニム和は、２進数表示で各桁の１の個数が奇数のとき１、偶数の時０でもあるので、ニム和が０でないということは、ｓの各桁のうち１のものが必ずあります。（本文では最下位） このうち、一番位が高い桁（下から数えて第ｎ位とします）について考えると、ニム和が１なので、同じ桁に１となるものが、ａ、ｂ、ｃ、ｄ、ｅの中に少なくとも１つはあります。（全て０ならニム和も０） 例えば、ａがそうだとします。（本文では、ａ＝１、ｃ＝３、ｅ＝５） ａ’＝ａ＋ｓとすると、 ｓ’＝ａ’＋ｂ＋ｃ＋ｄ＋ｅ 　　＝（ａ＋ｓ）＋ｂ＋ｃ＋ｄ＋ｅ 　　＝（ａ＋ｂ＋ｃ＋ｄ＋ｅ）＋ｓ 　　＝ｓ＋ｓ 　　＝０ になります。 ここで、 　・ｓの第ｍ位の桁（ｍ＞ｎ）は０だから、ａ’＝ａ＋ｓではａと同じ、 　・第ｎ位は、ａもｓも１なので、ａ’＝ａ＋ｓでは０ 従って、ａ’＝ａ＋ｓ＜ａとなります。（本問では、１＋ｓ＝０、３＋ｓ＝２、５＋ｓ＝４） すなわち、ａ→ａ’個に減らせば、ｓ’＝０となり、ニム和を０にすることができます。 今度は、後手番でニム和が０とします。 後手が、ａ、ｂ、ｃ、ｄ、ｅのいずれかの碁石を減らしたとき（例えばｂ→ｂ’個）、 ｂ’の各桁のうち、１個はｂと値が異なるものがあります。 すると、その桁ではｂ→ｂ’に伴って０→１か１→０になっています。 ａ、ｂ’、ｃ、ｄ、ｅについていえば、前者では１の個数は＋１、後者では−１になるのでいずれのときも、偶数→奇数に変わります。 従って、ｓ’＝ａ＋ｂ’＋ｃ＋ｄ＋ｅは０ではありません。 よって、その次の先手番では再びニム和を０になるよう碁石を減らすことができます。 以上を繰り返していけば、碁石の数は次第に減っていき、後手番で全て０の場合に必ずなってしまうので、必ず先手勝ちとすることができます。

---