第１４５問の解答

---

１．問題　［平面図形］

下図のＡＢＣＤは菱形です。 さて、面積は何ｃｍ2あるでしょうか。

---

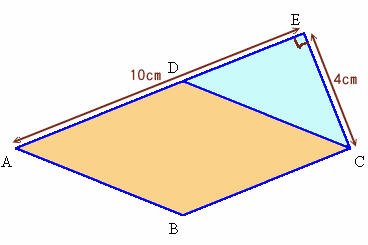２．解答例１(ヒデー王子さん、ありっちさん、長野美光さん、他)

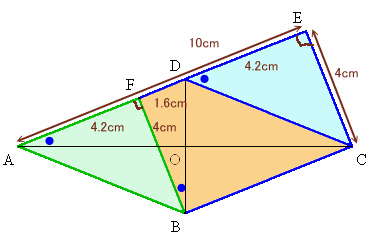
問題図の直角の部分をＥ、ＣからＡＣに垂直に立てた直線と、ＡＥの延長との交点をＦ、および菱形の中心をＯとします。

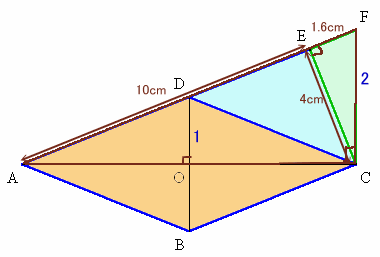
△ＣＦＥ∝△ＡＣＥより、
　ＥＦ＝ＥＣ×ＥＣ／ＡＥ＝４×４／１０＝１．６ｃｍ。

△ＡＤＯ∝△ＡＦＣより、ＤＯ：ＦＣ＝ＡＯ：ＡＣ＝１：２。
よって、菱形ＡＢＣＤ
　　＝△ＡＤＣ×２
　　＝△ＡＦＣ　　（底辺が等しく、高さが２倍）
　　＝1/2×ＡＦ×ＥＣ
　　＝1/2×１１．６×４
　　＝２３．２ｃｍ²。

答：２３．２ｃｍ²

以上

---

３．解答例２(自転車小僧さん、他)

問題図の直角部分をＥ、およびＢからＡＥに下ろした垂線の足をＦとします。

ＢＣＥＦは長方形になるので、ＢＦ＝ＥＣ＝４ｃｍ。

∠ＤＢＦ＝∠ＣＡＥなので、△ＤＢＦ∝△ＣＡＥ。
よって、ＤＦ＝ＢＦ×ＣＥ／ＡＥ＝４×４／１０＝１．６ｃｍ。

∠ＣＡＥ＝∠ＣＤＥ、ＡＢ＝ＤＣより、△ＡＢＦ≡△ＤＣＥ。
よって、ＡＦ＝ＤＥ＝（ＡＥ−ＤＦ）／２＝（１０−１．６）／２＝４．２ｃｍ。

よって、菱形ＡＢＣＤ＝ＡＤ×ＢＦ＝５．８×４＝２３．２ｃｍ²。

---

４．解答例３(AUさん、中村明海さん、noetherさん、うっしーさん、N.Nishiさん、あんみつさん、大沢幸一さん、他)

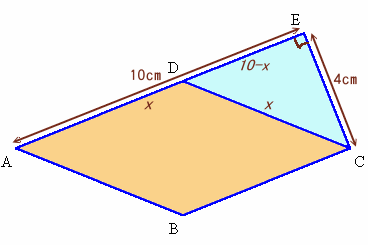
問題図の直角部分をＥ、ＡＤ＝ｘとします。

ＤＥ＝１０−ｘ、ＤＣ＝ｘなので、
　（１０−ｘ）²＋４²＝ｘ²より、
　１００−２０ｘ＋ｘ²＋１６＝ｘ²
よって、ｘ＝５．８を得ます。

菱形ＡＢＣＤ＝ＡＤ×ＥＣ＝５．８×４＝２３．２ｃｍ²。

---

５．解答例４(杉本未来さん、他)

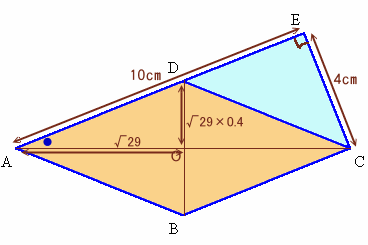
三平方の定理より、ＡＣ²＝ＡＥ²＋ＥＣ²＝１０²＋４²＝１１６。
よって、ＡＣ＝√１１６＝２√２９、ＡＯ＝ＡＣ／２＝√２９。

∠ＣＡＥが共通だから△ＡＤＯ∝△ＡＣＥ、
よって、ＤＯ＝ＡＯ×４／１０＝√２９×０．４。

よって、菱形ＡＢＣＤ
　＝△ＡＤＯ×４
　＝ＡＯ×ＤＯ×２
　＝√２９×√２９×０．４×２
　＝２９×０．８
　＝２３．２ｃｍ²。

---