第１４６問の解答

１．問題　［規則性］

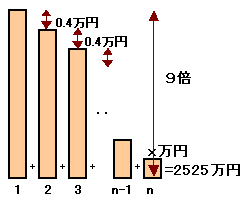
某算数サイトでは、賞金総額２５２５万円をかけた算数ニコニコ選手権を開催することになりました。
参加者全員に順位をつけ（同順位は無し）、１位の人にもっとも多くの賞金を与えました。
２位になった人には、１位の人より４０００円少なく、３位の人には２位の人より４０００円少なく、・・・、と４０００円ずつ減額しながら参加者全員に配分したところ、最下位の人の賞金は１位の人の９分の１になり、用意した２５２５万円はちょうど使い切ったそうです。

さて、この大会の参加者は何人だったでしょう？

２．解答例１(杉本未来さん、たなかさん、すうぱあさん、ふぇるまーさん、大岡敏幸さん、DrKさん、他多数)


最下位の賞金をｘ万円、人数をｎとします。

参考図1

題意より、x+0.4×(n-1)=9x　
よって、　x=(n-1)/20　・・・　（１）

また、Σ{x+0.4×(k-1)}＝2525
　　nx+0.4×(n-1)n/2=2525　

（１）を代入して、
　　n(n-1)/20+4×(n-1)n/20=2525
よって、n(n-1)=2525×4=10100
　　n2-n-10100=0
 　(n-101)(n+100)=0
よって、n=101を得る。　

　

答：１０１人

以上

３．解答例２(香川仁志さん、ＡЯＯＴさん、ありっちさん、中村明海さん、他)

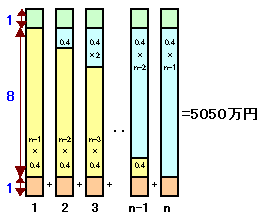
全体を２倍すると全員が同じ賞金になります。

参考図2

0.4万円の合計は全体の8/10だから
　２５２５万×8/10÷0.4＝５０５０
５０５０は１から１００までの整数の和だから、差額は100人分。
従って、全体の人数は、100＋１＝101人となります。