第１４９問の解答

１．問題　［平面図形］

問題図

三角形ＡＢＣのＡＢ上にＰ、ＡＣ上にＱを取り、２本の線ＰＣとＱＢを引きます。また、その交点をＯとします。

このとき、各部分の面積が、
　・△ＰＢＯ：２８ｃｍ2
　・△ＯＢＣ：１６ｃｍ2
　・△ＱＣＯ：８ｃｍ2
となりました。

では、この三角形ＡＢＣ全体の面積は何ｃｍ2あるでしょう。

　

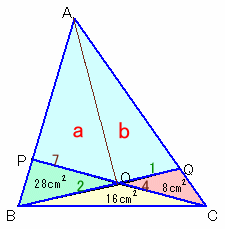
２．解答例１( ヒデー王子さん、長野美光さん、萬田銀次郎さん、うっしーさん、有無相生さん、ハラギャーテイさん、N.Nishiさん、他多数)

△APO＝ａ、△AOQ＝ｂとおきます。 

参考図1

ＰＯ：ＯＣ＝△ＰＢＯ：△ＯＢＣ＝７：４。
よって、△ＡＰＯ：△ＡＯＣ＝ａ：ｂ+8＝７：４、
従って、４ａ=７ｂ+５６　・・・（１）

ＢＯ：ＯQ＝△ＯＢＣ：△ＱＯＣ＝２：１。
よって、△ＡＢＯ：△ＡＯＱ＝ａ＋２８：ｂ＝２：１、
従って、２ｂ=ａ＋２８　・・・（２）

（１）、（２）より、ａ＝３０８、ｂ＝１６８。
よって、
△ＡＢＣ＝ａ＋ｂ＋２８＋１６＋８＝３０８＋１６８＋５２＝５２８ｃｍ2。

算数的には（長野美光さんによる）、△ＡＯＣ＝４とおくと、 
△ＡＯＰ＝７。

△ＯＢＣ：△ＱＯＣ＝△ＡＢＯ：△ＡＯＱ＝２：１より、
△ＯＢＣ＋△ＡＢＯ：△ＱＯＣ＋△ＡＯＱ＝四角形ＡＢＣＯ：△ＡＯＣ＝２：１。
よって、四角形ＡＢＣＯ＝８。
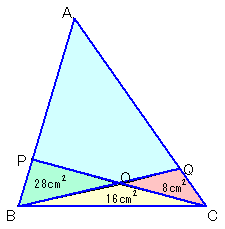
従って、△ＰＢＣ＝四角形ＡＢＣＯ−△ＡＯＰ＝８−７＝１。

△ＰＢＣ＝２８＋１６＝４４ｃｍ2なので、
△ＡＢＣ＝４４×（１＋４＋７）＝４４×１２＝５２８ｃｍ2。

答：５２８ｃｍ2

以上

３．解答例２(高田修成さん、Miki Sugimotoさん、他多数)

ＡＢ／ＰＢ＝ｐ、ＡＣ／ＱＣ＝ｑとおきます。

△ＡＰＣと直線ＢＱについて、メネラウスの定理より、
　（ＡＢ/ＢＰ）・（ＰＯ/ＯＣ）・（ＣＱ/ＱＡ）＝１
　ｐ・（７/４）・（１/ｑ−１）＝１
よって、７ｐ＝４ｑ−４　・・・（３）

△ＡＢＱと直線ＰＣについて、メネラウスの定理より、
　（ＡＰ/ＰＢ）・（ＢＯ/ＯＱ）・（ＱＣ/ＣＡ）＝１
　（ｐ−１）・（２/１）・（１/ｑ）＝１
よって、２ｐ−２＝ｑ　・・・（４）

（３）、（４）より、ｐ＝１２、ｑ＝２２を得る。
よって、△ＡＢＣ＝△ＰＢＣ×ｐ＝４４×１２＝５２８ｃｍ2。

　

４．解答例３

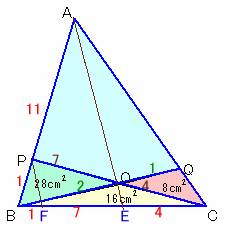
ＡＯの延長線とＢＣとの交点をＥとし、ＰからＡＥに引いた直線とＢＣの交点をＦとする。

参考図2

ＦＥ：ＥＣ＝ＰＯ：ＯＣ＝７：４。
ＢＥ：ＥＣ＝ＢＯ：ＯＱ＝２：１＝８：４。
よって、ＢＦ＝１。
従って、ＢＰ：ＰＡ＝ＢＦ：ＦＣ＝１：１１。

よって、△ＡＢＣ＝△ＰＢＣ×１２＝４４×１２＝５２８ｃｍ2。

他の解法としては、

  • ベクトルを用いる：BossFさん他

  • 座標を用いる：ταροさん他

  • 重心と面積比による：LIONさん他

  • ＣからＡＢに垂線を引く：DrKさん他

などがありました。